Cho phương trình:\[{x^2} + 3x - 10 = 0\] có \[2\]nghiệm\[{x_1},{x_2}\]. Tính giá trị biểu thức \[A = \frac{{{x_1} + 2}}{{{x_2}}} + \frac{{{x_2} + 2}}{{{x_1}}}\]

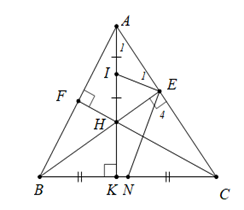
a) Chứng minh bốn điểm \(A\), \(E\), \(H\), \(F\) nằm trên cùng một đường tròn.

Ta có \[\widehat {AEB} = 90^\circ \](do \(BE\) là đường cao của \(\Delta ABC\)) hay \[\widehat {AEH} = 90^\circ \]

\[\widehat {AFC} = 90^\circ \] (do \(CF\) là đường cao của \(\Delta ABC\)) hay \[\widehat {AFH} = 90^\circ \]

Suy ra bốn điểm \(A,E,H,F\) cùng nằm trên một đường tròn đường kính \(AH\) (đpcm)

b) Chứng minh \(NE\) là tiếp tuyến của đường tròn đường kính \(AH\);

Vì \(I\) là trung điểm của đoạn thẳng \(AH\) nên \(I\) là tâm đường tròn đường kính \(AH\)

Suy ra \(IA = IE\)

Vì\(\Delta IAE\) cân tại \(I\) nên \({\widehat A_1} = {\widehat E_1}\)                            (1)

\[\Delta EBC\] vuông tại \[E\]có \[EN\] là đường trung trrung tuyến ứng với cạnh huyền \[BC\]

Nên \(EN = NC\,\,\,\left( { = \frac{{BC}}{2}} \right)\)

Suy ra \[\Delta ENC\] cân tại \[N\] nên \(\widehat {NCE} = \widehat {{E_4}}\)                (2)

Xét \[\Delta AKC\] vuông tại \[K\] có \[\widehat {KCA} + {\widehat A_1} = 90^\circ \] hay \[\widehat {NCE} + {\widehat A_1} = 90^\circ \]        (3)

Từ (1), (2), (3) suy ra \({\widehat E_1} + {\widehat E_4} = 90^\circ \)

Lại có  \({\widehat E_1} + {\widehat E_4} + \widehat {IEN} = 180^\circ \)  (do \(A;\;E;\;C\) thẳng hàng)

Suy ra \(90^\circ  + \widehat {IEN} = 180^\circ \)hay\(\widehat {IEN} = 90^\circ \)

Suy ra \(EN \bot EI\) tại \(E\)

Do đó \(NE\) là tiếp tuyến của đường tròn đường kính \(AH\)  (đpcm)

c) Chứng minh \[C{I^2} - I{E^2} = CK\;.\;CB\].

Áp dụng định lí Py – Ta – Go \(\Delta CIK\) vuông tại \(K\), ta có: \(C{I^2} = C{K^2} + I{K^2}\)       

Lại có \(IA = IE = IH\) (cùng bán kính đường tròn tâm I)

Suy ra \[C{I^2} - I{E^2} = C{K^2} + I{K^2} - I{E^2}\]

\[C{I^2} - I{E^2} = C{K^2} + (IK + IE)(IK - IE)\]

\[C{I^2} - I{E^2} = C{K^2} + (IK + IE)(IK - IH)\]  \[ = C{K^2} + AK\;.\;KH\]  \(\left( 4 \right)\)

Ta lại có \[CK.CB = CK(CK + KB)\] \[ = C{K^2} + CK\;.\;KB\]   \(\left( 5 \right)\)

Xét  \(\Delta KBH\) và \(\Delta KAC\) có

\(\widehat {KBH} = \widehat {KAC}\) (\( = 90^\circ  - \widehat {ACB}\));  \[\widehat {BKH} = \widehat {AKC} = 90^\circ \]

Do đó \[\left( {g - g} \right)\]

Nên \(\frac{{KB}}{{KA}} = \frac{{KH}}{{KC}}\) suy ra\(KA\;.\;KH = KB\;.\;KC\) hay \(AK\;.\;KH = CK\;.\;KB\)                  \(\left( 6 \right)\)

Từ \[\left( 4 \right)\],\(\left( 5 \right)\) và \(\left( 6 \right)\) suy ra \[C{I^2} - I{E^2} = CK\;.\;CB\]  (đpcm)

Gọi giá nhập về của chiếc ti vi là \(x\)(đồng). Theo đề cửa hàng thu lãi \(\frac{x}{{10}}\), tức là giá đã bán là \(x + \frac{x}{{10}}\). Nếu cửa hàng tiếp tục nâng giá bán chiếc tivi đó thêm \(5\% \)giá đã bán và bớt cho khách hàng 245 000 đồng, khi đó giá bán ra là \(x + \frac{x}{{10}} + \frac{5}{{100}}\left( {x + \frac{x}{{10}}} \right) - 245000\)

Theo đề khi đó cửa hàng thu lãi là 12% của giá nhập về nên ta có phương trình :

\(x + \frac{x}{{10}} + \frac{5}{{100}}\left( {x + \frac{x}{{10}}} \right) - 24\,500 = x + \frac{{12}}{{100}}x\)

Từ đó tính được \(x = 7\,000\,000\)

Vậy giá nhập về của chiếc ti vi đó là 7 triệu đồng.