(4,0 điểm)
Người ta đặt một khối nón vào trong một khối lập phương cạnh \(1\,m\) chứa đầy nước. Biết rằng đỉnh khối nón trùng với tâm một mặt của khối lập phương, đáy khối nón tiếp xúc với các cạnh của mặt đối diện. Tính thể tích lượng nước trong khối bị tràn ra ngoài. (Lấy \(\pi \approx 3,14,\) kết quả làm tròn đến hai chữ số thập phân)
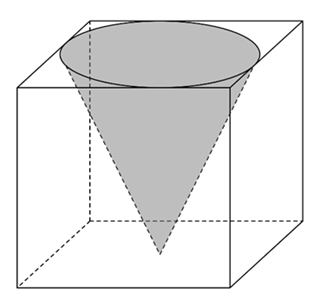
Người ta đặt một khối nón vào trong một khối lập phương cạnh \(1\,m\) chứa đầy nước. Biết rằng đỉnh khối nón trùng với tâm một mặt của khối lập phương, đáy khối nón tiếp xúc với các cạnh của mặt đối diện. Tính thể tích lượng nước trong khối bị tràn ra ngoài. (Lấy \(\pi \approx 3,14,\) kết quả làm tròn đến hai chữ số thập phân)

Quảng cáo
Trả lời:
Thể tích lượng nước trong khối hộp bị tràn ra ngoài là thể tích của khối nón.
\(V = \frac{1}{3}\pi {R^2}h \approx \frac{1}{3} \cdot 3,14.{\left( {\frac{1}{2}} \right)^2} \cdot 1 \approx 0,26\,\,\,({m^2})\)
Vậy lượng nước bị trào ra có thể tích \( \approx 0,26\,\,\,({m^2})\).
Câu hỏi cùng đoạn
Câu 2:
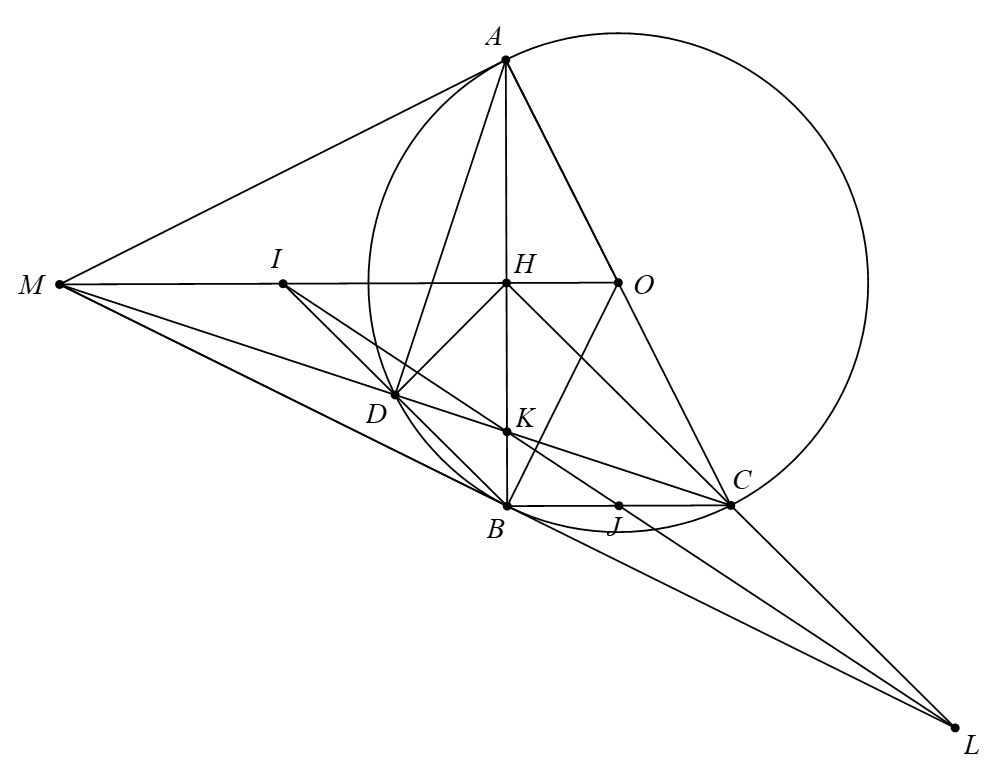
Từ điểm M nằm ngoài đường tròn \[\left( O \right)\], kẻ các tiếp tuyến \[MA,{\rm{ }}MB\] với \[\left( O \right)\] (\[B,{\rm{ }}C\] là các tiếp điểm). Kẻ đường kính \[AC\] của \[\left( O \right)\]. Đoạn thẳng \[MC\] cắt \[AB\] tại \[K\] và cắt đường tròn \[\left( O \right)\] tại điểm thứ hai \[D\]. Gọi \[I,{\rm{ }}H\] lần lượt là các giao điểm của \[MO\] với \[BD,{\rm{ }}AB.\]
a) Chứng minh bốn điểm \[M,{\rm{ }}A,{\rm{ }}O,{\rm{ }}B\] cùng thuộc một đường tròn.
b) Chứng minh \[MO\] song song với \[BC\] và \(I{M^2} = ID.IB\).
c) Gọi \[L\] là giao điểm của \[IK,{\rm{ }}HC\]. Chứng minh ba điểm \[M,{\rm{ }}B,{\rm{ }}L\] thẳng hàng.
Từ điểm M nằm ngoài đường tròn \[\left( O \right)\], kẻ các tiếp tuyến \[MA,{\rm{ }}MB\] với \[\left( O \right)\] (\[B,{\rm{ }}C\] là các tiếp điểm). Kẻ đường kính \[AC\] của \[\left( O \right)\]. Đoạn thẳng \[MC\] cắt \[AB\] tại \[K\] và cắt đường tròn \[\left( O \right)\] tại điểm thứ hai \[D\]. Gọi \[I,{\rm{ }}H\] lần lượt là các giao điểm của \[MO\] với \[BD,{\rm{ }}AB.\]
a) Chứng minh bốn điểm \[M,{\rm{ }}A,{\rm{ }}O,{\rm{ }}B\] cùng thuộc một đường tròn.
b) Chứng minh \[MO\] song song với \[BC\] và \(I{M^2} = ID.IB\).
c) Gọi \[L\] là giao điểm của \[IK,{\rm{ }}HC\]. Chứng minh ba điểm \[M,{\rm{ }}B,{\rm{ }}L\] thẳng hàng.
a) \(MA,\,MB\) là hai tiếp tuyến của \[\left( O \right)\]nên : \(MA \bot OA;\,MB \bot OB\)
- Xét \(\Delta MAO\) có \(\widehat {MAO} = 90^\circ \) nên 3 điểm \(A,\,M,\,O\) cùng thuộc đường tròn đường kính \(OM\)
- Xét \(\Delta MBO\) có \(\widehat {MBO} = 90^\circ \) nên 3 điểm \(B,\,M,\,O\) cùng thuộc đường tròn đường kính \(OM\)
Vậy bốn điểm \[M,{\rm{ }}A,{\rm{ }}O,{\rm{ }}B\] cùng thuộc một đường tròn. (ĐPCM)
b) Ta có:\(MA = MB\) (\(MA,\,MB\) là hai tiếp tuyến của \[\left( O \right)\])
\(OA = OB = R\)
Nên \(OM\)là trung trực của \(AB\) hay \(OM \bot AB\) tại \(H\)
Mà \(B\) thuộc đường tròn đường kính \(AC\)nên \(\widehat {ABC} = 90^\circ \) hay \(BC \bot AB\)
Suy ra: \(MO//BC\)
\(\widehat {IMD} = \widehat {BCD}\) (2 góc so le trong)
Lại có: \(\widehat {MBI} = \widehat {BCD}\) nên \[\widehat {IMD} = \widehat {IBM} = \widehat {BCD}\]
Xét \(\Delta IMD\) và \(\Delta IBM\) có :
\(\widehat {MIB}\) chung
\[\widehat {IMD} = \widehat {IBM}\]
Nên: \[\Delta IMD \sim \Delta IBM\] (g.g)
Suy ra: \[\frac{{IM}}{{IB}} = \frac{{ID}}{{IM}}\] hay \[I{M^2} = IB.ID\](ĐPCM)
c) Ta có \(\widehat {ADC} = 90^\circ \) nên \(\widehat {ADM} = 90^\circ \)
Suy ra 3 điểm \(A,\,D,\,M\) cùng thuộc đường tròn đường kính \(AM\).
Mà \(\widehat {AHM} = 90^\circ \)nên 3 điểm \(A,\,H,\,M\) cùng thuộc đường tròn đường kính \(AM\).
Suy ra bốn điểm \(A,\,D,\,H,\,M\) cùng thuộc đường tròn đường kính \(AM\).
Hay \(AMDH\) là tứ giác nội tiếp nên \(\widehat {IHD} = \widehat {MAD}\)
Mà \(\widehat {MAD} = \widehat {ABD}\) nên \(\widehat {IBH} = \widehat {IHD}\)
Xét \(\Delta IHD\) và \(\Delta IBH\) có:
\(\widehat {IHD} = \widehat {IBH}\) (cmt)
\(\widehat {HIB}\) chung
Nên: \(\Delta IHD \sim \Delta IBH\), suy ra \(I{H^2} = IB.ID\)
Mà \(I{M^2} = IB.ID\)nên \(IM = IH\)
Gọi \(J\) là giao điểm của \(IL\) và \(BC\)
Xét \(\Delta MKI\) có \(IM{\rm{//}}CJ\) nên \(\frac{{JC}}{{IM}} = \frac{{KJ}}{{KI}}\)
Xét \(\Delta IKH\) có \(BJ{\rm{//}}IH\) nên \(\frac{{BJ}}{{IH}} = \frac{{KJ}}{{KI}}\)
Suy ra : \(JC = JB\)
Hay \(J\) là trung điểm của \(BC\)
Xét \(\Delta ILH\) có \(CJ{\rm{//}}LH\) nên \(\frac{{LC}}{{LH}} = \frac{{CJ}}{{HI}} = \frac{{2CI}}{{2HJ}} = \frac{{CB}}{{MH}}\)
Lại có \(\widehat {MHL} = \widehat {BCL}\) (đồng vị)
Suy ra \(\Delta MHL \sim \Delta BCL\) (c.g.c)
Từ đó ta có: \(\widehat {HLB} = \widehat {HLM}\)
Vậy \(M,B,\,L\) thẳng hàng.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
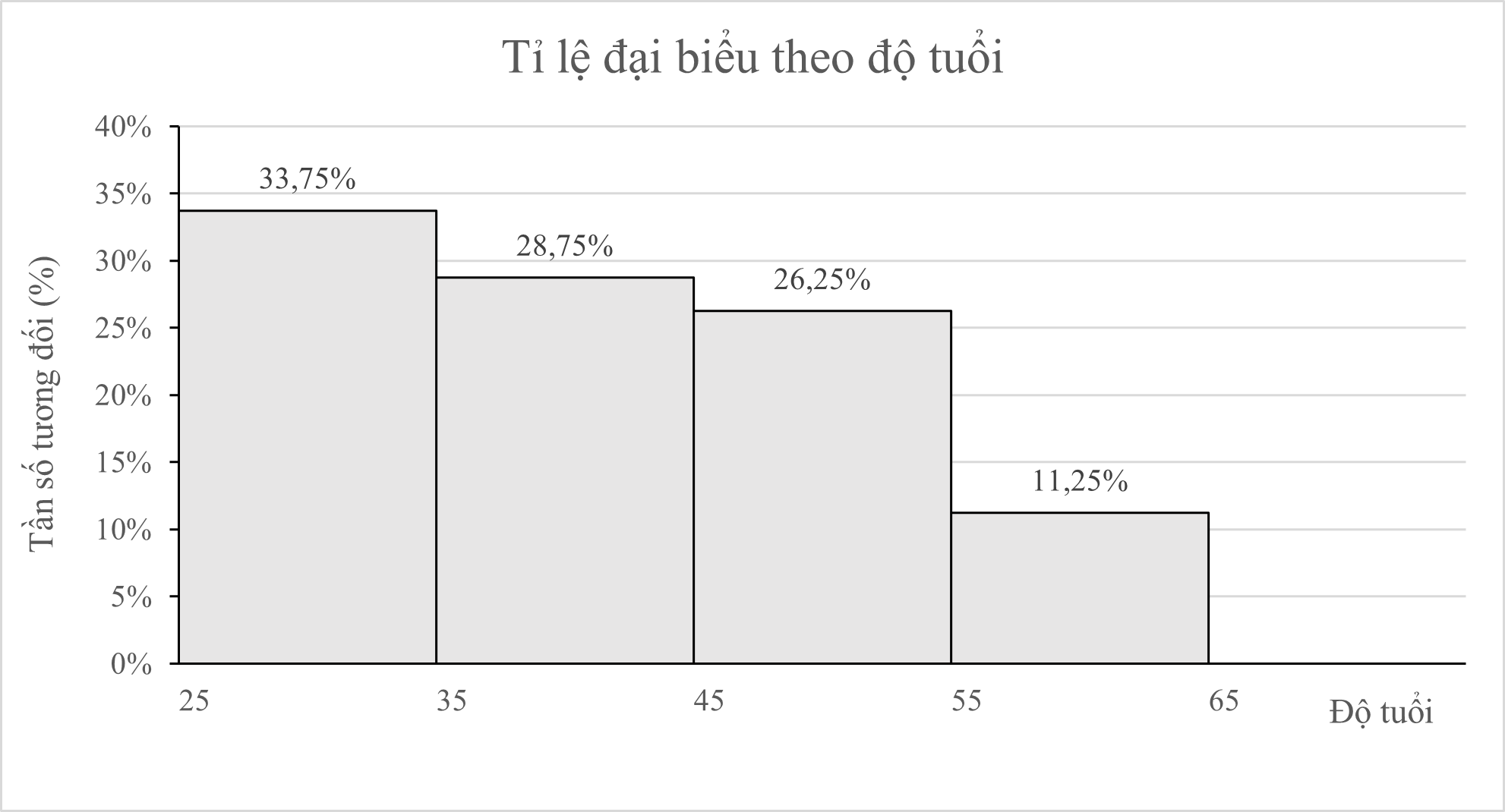
a) Nhóm [25; 35) chiếm 33,75% so với tổng số đại biểu và có 54 người.
Suy ra số người tham dự hội nghị là 54: 33,75% = 160 (người)
Vậy tổng số đại biểu tham dự hội nghị là 160 người.
b) Tổng số % số đại biểu tham dự hội nghị dưới 45 tuổi là:
\[33,75\% + 28,75\% = 62,5\% > 50\% .\]
Vậy nhận định “Trên 50% số đại biểu tham dự hội nghị dưới 45 tuổi” “ là đúng.
Lời giải
Gọi giá tiền của bàn là và quạt điện theo giá niêm yết lần lượt là: \(x;\,y\) (đơn vị: nghìn đồng; điều kiện \(0 < x;\,y < 850\)).
Do tổng số tiền mua bàn là và quạt điện theo giá niêm yết là \[850\] nghìn đồng nên ta có phương trình: \(x + y = 850\) (1).
Bàn là giảm giá 20% nên số tiền cần trả cho bàn là là: \(x - \frac{{20}}{{100}}x = \frac{4}{5}x\) (nghìn đồng).
Quạt điện giảm giá 10% nên số tiền trả cho quạt điện là: \(y - \frac{{10}}{{100}}y = \frac{9}{{10}}y\) (nghìn đồng).
Tổng số tiền phải trả theo giá khuyến mại là \[740\] nghìn nên ta có phương trình:
\(\frac{4}{5}x + \frac{9}{{10}}y = 740\) (2)
Từ (1) và (2) ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + y = 850\,\,\,\,\,\,\,\,\,\,}\\{\frac{4}{5}x + \frac{9}{{10}}y = 740}\end{array}} \right.\)
Giải hệ ta được \(\left\{ {\begin{array}{*{20}{c}}{x = 250}\\{y = 500}\end{array}} \right.\) (thỏa mãn điều kiện)
Vậy giá tiền của bàn là là \[250\] nghìn đồng, của quạt điện là \[600\] nghìn đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.