(1,5 điểm)

Biểu đồ bên biểu diễn tỉ lệ đại biểu tham dự hội nghị theo độ tuổi. Biết rằng có \[54\] đại biểutừ \[25\] đến \[35\]tuổi.
           

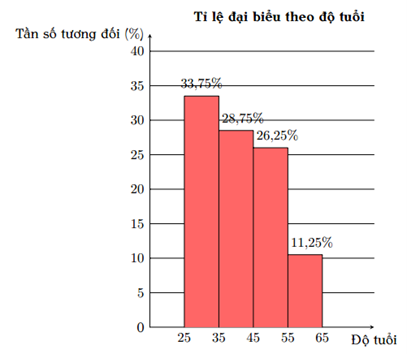Có bao nhiêu đại biểu tham dự hội nghị? Lập bảng tần số ghép nhóm tương ứng.

Gọi số tấm kính giọt bắn mỗi lớp \(9A,\;9B\)làm được trong đợt 1 lần lượt là: \(x,\;y\) (tấm) (\(0 < x,y < 1500)\)

Vì trong đợt 1 cả hai lớp \(9A,\;9B\) đã làm được \(1500\)chiếc tấm kính chắn giọt bắn nên ta có phương trình:

\(x + y = 1500\)  (1)

Số tấm kính giọt bắn lớp \(9A\)làm được trong đợt 2 là: \(x + 70\% .x = 1,7x\) (tấm)

Số tấm kính giọt bắn lớp \(9B\)làm được trong đợt 2 là: \(y + 68\% .y = 1,68y\) (tấm)

Vì trong đợt 2 cả hai lớp \(9A,\;9B\) đã làm được \(2358\)chiếc tấm kính chắn giọt bắn nên ta có phương trình:

\(1,7x + 1,68y = 2358\)  (2)

Từ (1) và (2) ta có hệ phương trình:\(\left\{ \begin{array}{l}x + y = 1500\quad \quad \quad \quad \quad \left( 1 \right)\\1,7x + 1,68y = 2358\quad \quad \left( 2 \right)\end{array} \right.\)

Giải hệ phương trình ta được: \(x = 960\;\left( {TM} \right);\;y = 540\;\left( {TM} \right)\)

Vậy số tấm kính giọt bắn mỗi lớp \(9A,\;9B\)làm được trong đợt 1 lần lượt là: \(960;\;540\) (tấm)

Gọi chiều rộng là \(x\left( {cm} \right)\left( {0 < x < 12} \right)\)

Chiều dài là \(12 - x\left( {cm} \right)\)

Chiều cao là \(24 - x\left( {cm} \right)\)

Ta có thể tích chiếc hộp là: \(V = x\left( {12 - x} \right)\left( {24 - x} \right)\left( {c{m^3}} \right)\)

Bất đẳng thức Cauchy 3 số không âm \(a,b,c\)ta có:  \(a + b + c \ge 3\sqrt[3]{{abc}}\)      

Dấu “=” xảy ra khi và chỉ khi \(a = b = c\)

Thật vậy, đặt \(x = \sqrt[3]{a},y = \sqrt[3]{b},z = \sqrt[3]{c}\)\( \Rightarrow x,y,z \ge 0 \Rightarrow x + y + z \ge 0\)

Ta phái chứng minh:

\({x^3} + {y^3} + {z^3} \ge 3xyz\)

\({\left( {x + y} \right)^3} - 3xy\left( {x + y} \right) + {z^3} - 3xyz \ge 0\)

\(\left( {x + y + z} \right)\left[ {{{\left( {x + y} \right)}^2} - \left( {x + y} \right)z + {z^2}} \right] - 3xy\left( {x + y + z} \right) \ge 0\)

\(\left( {x + y + z} \right)\left[ {{x^2} + {y^2} + {z^2} + 2xy - xz - yz} \right] - 3xy\left( {x + y + z} \right) \ge 0\)

\(\left( {x + y + z} \right)\left[ {{x^2} + {y^2} + {z^2} - xy - xz - yz} \right] \ge 0\)

\({x^2} + {y^2} + {z^2} - xy - xz - yz \ge 0\)  (vì \(x + y + z \ge 0\))

\({\left( {x - y} \right)^2} + {\left( {y - z} \right)^2} + {\left( {z - x} \right)^2} \ge 0\)\(\)(luôn đúng)

Dấu “=” xảy ra khi \(x = y = z\) hay \(a = b = c\)

Áp dụng bất đẳng thức Cauchy cho 3 số không âm ta có:

\(V = x\left( {12 - x} \right)\left( {24 - x} \right)\left( {c{m^3}} \right)\)

\(\frac{1}{{\left( {\sqrt 3  - 1} \right)\left( {2 - \sqrt 3 } \right)}}.x.\left( {\sqrt 3  - 1} \right)\left( {2 - \sqrt 3 } \right)\left( {12 - x} \right)\left( {24 - x} \right)\)

\( \le \frac{1}{{\left( {\sqrt 3  - 1} \right)\left( {2 - \sqrt 3 } \right)}}.{\left[ {\frac{{x + \left( {\sqrt 3  - 1} \right)\left( {12 - x} \right) + \left( {2 - \sqrt 3 } \right)\left( {24 - x} \right)}}{3}} \right]^3}\)

\( = \frac{1}{{\left( {\sqrt 3  - 1} \right)\left( {2 - \sqrt 3 } \right)}}.{\left[ {\frac{{x + 12\sqrt 3  - \sqrt 3 x - 12 + x + 48 - 2x - 24\sqrt 3  + \sqrt 3 x}}{3}} \right]^3}\)

\( = \frac{1}{{\left( {\sqrt 3  - 1} \right)\left( {2 - \sqrt 3 } \right)}}.{\left[ {\frac{{36 - 12\sqrt 3 }}{3}} \right]^3} = 384\sqrt 3 \)

 Dấu “=” xảy ra khi và chỉ khi: \(x = \left( {\sqrt 3  - 1} \right)\left( {12 - x} \right)\)\( = \left( {2 - \sqrt 3 } \right)\left( {24 - x} \right)\)\( \Leftrightarrow x = 12 - 4\sqrt 3 \)

Vậy \({V_{\max }} = 384\sqrt 3 \)\( \Leftrightarrow x = 12 - 4\sqrt 3 \)