(2,5 điểm)

Hưởng ứng phong trào của hội đồng đội làm tấm kính chắn giọt bắn gửi các y bác sĩ chốngdịch. Hai lớp \(9A,\;9B\) trong đợt 1 đã làm được \(1500\) chiếc tấm kính chắn giọt bắn. Để đáp ứng nhu cầu với tình hình dịch bệnh, nên trong đợt 2 lớp \(9A\) vượt mức \(70\% \) và lớp \(9B\) vượt mức \(68\% \)nên cả hai lớp đã làm được \(2358\) chiếc tấm kính chắn giọt bắn. Hỏi trong đợt 1 mỗi lớp làm được bao nhiêu tấm kính chắn giọt bắn?

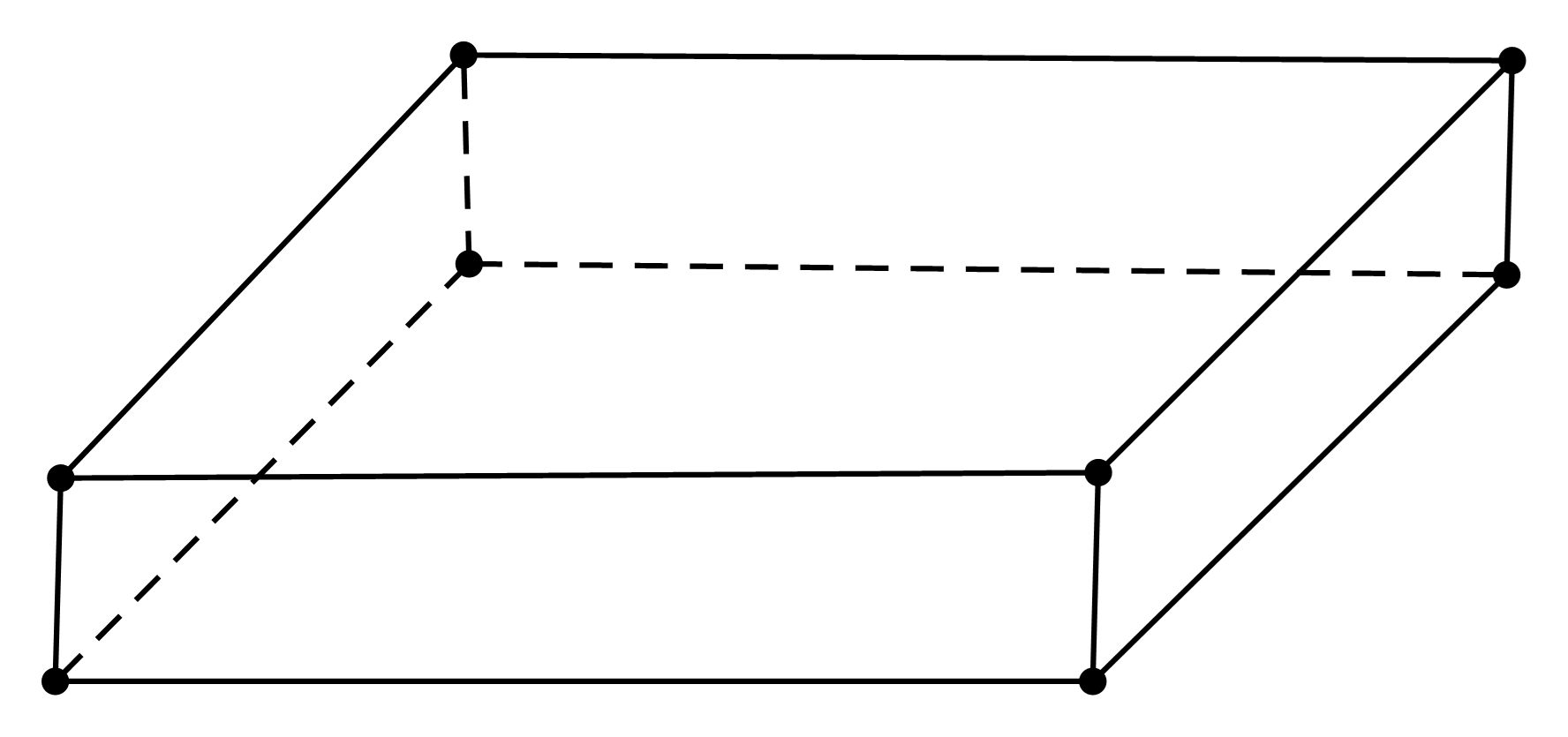
Gọi chiều rộng là \(x\left( {cm} \right)\left( {0 < x < 12} \right)\)

Chiều dài là \(12 - x\left( {cm} \right)\)

Chiều cao là \(24 - x\left( {cm} \right)\)

Ta có thể tích chiếc hộp là: \(V = x\left( {12 - x} \right)\left( {24 - x} \right)\left( {c{m^3}} \right)\)

Bất đẳng thức Cauchy 3 số không âm \(a,b,c\)ta có:  \(a + b + c \ge 3\sqrt[3]{{abc}}\)      

Dấu “=” xảy ra khi và chỉ khi \(a = b = c\)

Thật vậy, đặt \(x = \sqrt[3]{a},y = \sqrt[3]{b},z = \sqrt[3]{c}\)\( \Rightarrow x,y,z \ge 0 \Rightarrow x + y + z \ge 0\)

Ta phái chứng minh:

\({x^3} + {y^3} + {z^3} \ge 3xyz\)

\({\left( {x + y} \right)^3} - 3xy\left( {x + y} \right) + {z^3} - 3xyz \ge 0\)

\(\left( {x + y + z} \right)\left[ {{{\left( {x + y} \right)}^2} - \left( {x + y} \right)z + {z^2}} \right] - 3xy\left( {x + y + z} \right) \ge 0\)

\(\left( {x + y + z} \right)\left[ {{x^2} + {y^2} + {z^2} + 2xy - xz - yz} \right] - 3xy\left( {x + y + z} \right) \ge 0\)

\(\left( {x + y + z} \right)\left[ {{x^2} + {y^2} + {z^2} - xy - xz - yz} \right] \ge 0\)

\({x^2} + {y^2} + {z^2} - xy - xz - yz \ge 0\)  (vì \(x + y + z \ge 0\))

\({\left( {x - y} \right)^2} + {\left( {y - z} \right)^2} + {\left( {z - x} \right)^2} \ge 0\)\(\)(luôn đúng)

Dấu “=” xảy ra khi \(x = y = z\) hay \(a = b = c\)

Áp dụng bất đẳng thức Cauchy cho 3 số không âm ta có:

\(V = x\left( {12 - x} \right)\left( {24 - x} \right)\left( {c{m^3}} \right)\)

\(\frac{1}{{\left( {\sqrt 3  - 1} \right)\left( {2 - \sqrt 3 } \right)}}.x.\left( {\sqrt 3  - 1} \right)\left( {2 - \sqrt 3 } \right)\left( {12 - x} \right)\left( {24 - x} \right)\)

\( \le \frac{1}{{\left( {\sqrt 3  - 1} \right)\left( {2 - \sqrt 3 } \right)}}.{\left[ {\frac{{x + \left( {\sqrt 3  - 1} \right)\left( {12 - x} \right) + \left( {2 - \sqrt 3 } \right)\left( {24 - x} \right)}}{3}} \right]^3}\)

\( = \frac{1}{{\left( {\sqrt 3  - 1} \right)\left( {2 - \sqrt 3 } \right)}}.{\left[ {\frac{{x + 12\sqrt 3  - \sqrt 3 x - 12 + x + 48 - 2x - 24\sqrt 3  + \sqrt 3 x}}{3}} \right]^3}\)

\( = \frac{1}{{\left( {\sqrt 3  - 1} \right)\left( {2 - \sqrt 3 } \right)}}.{\left[ {\frac{{36 - 12\sqrt 3 }}{3}} \right]^3} = 384\sqrt 3 \)

 Dấu “=” xảy ra khi và chỉ khi: \(x = \left( {\sqrt 3  - 1} \right)\left( {12 - x} \right)\)\( = \left( {2 - \sqrt 3 } \right)\left( {24 - x} \right)\)\( \Leftrightarrow x = 12 - 4\sqrt 3 \)

Vậy \({V_{\max }} = 384\sqrt 3 \)\( \Leftrightarrow x = 12 - 4\sqrt 3 \)

 Bán kính quả bóng hình cầu là : \(r = 6,5:2\) \( = 3,25cm\)

 Diện tích bề mặt mỗi quả bóng là : \({S_{mc}} = 4\pi {r^2}\) \( = 4.\pi {,3,25^2}\) \( = 42,25\pi \,\left( {c{m^2}} \right)\)

Thể tích của mỗi quả bóng hình cầu là: \(V = \frac{4}{3}\pi {r^3}\) \( = \frac{4}{3}.\pi {.3,25^3}\) \( = \frac{{13,73125\pi }}{3}\,\left( {c{m^3}} \right)\)

b)     Tính diện tích xung quanh và thể tích của hộp bóng.

Bán kính hộp bóng hình trụ chính là bán kính của quả bóng hình cầu là: \(r = 6,5:2 = 3,25cm\)

Chiều cao của hộp bóng hình trụ là: \(h = 3.6,5 = 19,5\left( {cm} \right)\)

Diện tích xung quanh hộp bóng hình trụ là : \({S_{xq}} = 2\pi Rh\) \( = 2.\pi .3,25.19.5\) \( = 123,5\pi \,\left( {c{m^2}} \right)\)

Thể tích của hộp bóng hình trụ là: \[V = \pi {r^2}h\] \[ = \pi {.3,25^2}.19,5\] \[ = 205,96875\pi \,\left( {c{m^3}} \right)\]