(1,5 điểm) Cho hai biểu thức \(A = \frac{{x + 3}}{{\sqrt x - 2}}\) và \(B = \frac{{\sqrt x + 3}}{{\sqrt x - 2}} - \frac{{3\sqrt x + 6}}{{x - 4}}\) với \(x > 0,\,{\rm{ }}x \ne 4\)
1) Tính giá trị của biểu thức \(A\) khi \(x = 16\).
2) Rút gọn biểu thức \(B\).
3) So sánh biểu thức \(\frac{A}{B}\) với \(3\).
(1,5 điểm) Cho hai biểu thức \(A = \frac{{x + 3}}{{\sqrt x - 2}}\) và \(B = \frac{{\sqrt x + 3}}{{\sqrt x - 2}} - \frac{{3\sqrt x + 6}}{{x - 4}}\) với \(x > 0,\,{\rm{ }}x \ne 4\)
1) Tính giá trị của biểu thức \(A\) khi \(x = 16\).
2) Rút gọn biểu thức \(B\).
3) So sánh biểu thức \(\frac{A}{B}\) với \(3\).
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 41 !!
Quảng cáo
Trả lời:
1) Với \(x = 16\) (thoả mãn \(x > 0,\,{\rm{ }}x \ne 4\)) ta có \(A = \frac{{16 + 3}}{{\sqrt {16} - 2}}\)\( = \frac{{19}}{2}\). Vậy \(A = \frac{{19}}{2}\) khi \(x = 16\).
2) Với \(x > 0,\,{\rm{ }}x \ne 4\) ta có \(B = \frac{{\sqrt x + 3}}{{\sqrt x - 2}} - \frac{{3\sqrt x + 6}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}}\)
\( = \frac{{\left( {\sqrt x + 3} \right)\left( {\sqrt x + 2} \right) - 3\sqrt x - 6}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\)
\( = \frac{{x + 5\sqrt x + 6 - 3\sqrt x - 6}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\)\( = \frac{{\sqrt x \left( {\sqrt x + 2} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\)
\( = \frac{{\sqrt x }}{{\sqrt x - 2}}\)
Vậy với \(x > 0,\,{\rm{ }}x \ne 4\) thì \(B = \frac{{\sqrt x }}{{\sqrt x - 2}}\)
3) Ta có \(\frac{A}{B} = \frac{{x + 3}}{{\sqrt x - 2}}:\frac{{\sqrt x }}{{\sqrt x - 2}} = \frac{{x + 3}}{{\sqrt x }}\)
Xét \(\frac{A}{B} - 3 = \frac{{x + 3}}{{\sqrt x }} - 3 = \frac{{x - 3\sqrt x + 3}}{{\sqrt x }} = \frac{{{{\left( {\sqrt x - \frac{3}{2}} \right)}^2} + \frac{3}{4}}}{{\sqrt x }}\)
Với \(x > 0,\,{\rm{ }}x \ne 4\) thì \(\sqrt x > 0,\,\,{\left( {\sqrt x - \frac{3}{2}} \right)^2} + \frac{3}{4} > 0\) nên \(\frac{A}{B} - 3 > 0\). Suy ra \(\frac{A}{B} > 3\).
Vậy với \(x > 0,\,{\rm{ }}x \ne 4\) thì \(\frac{A}{B} > 3\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
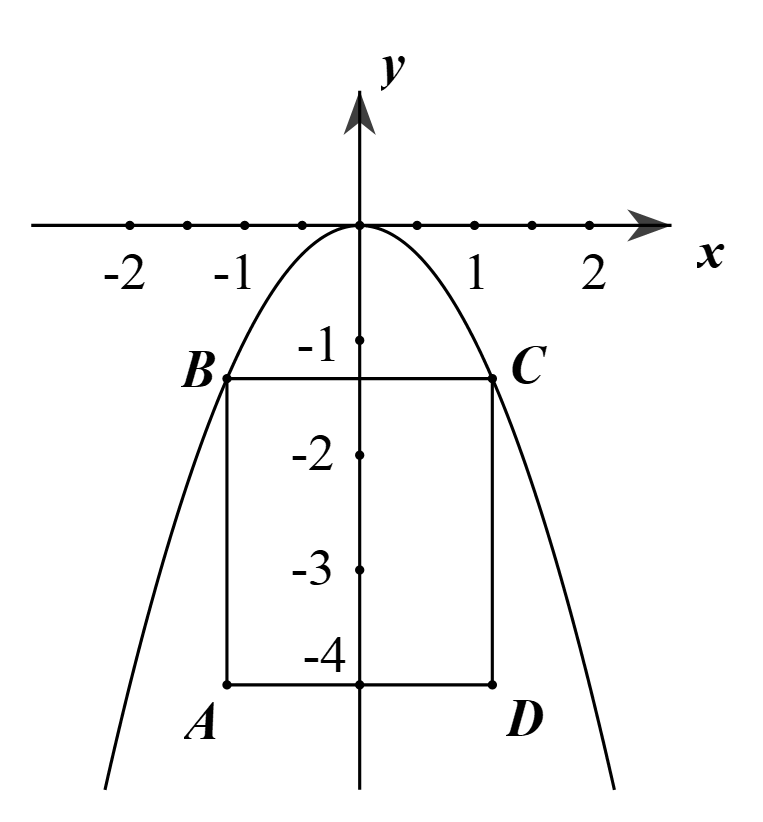
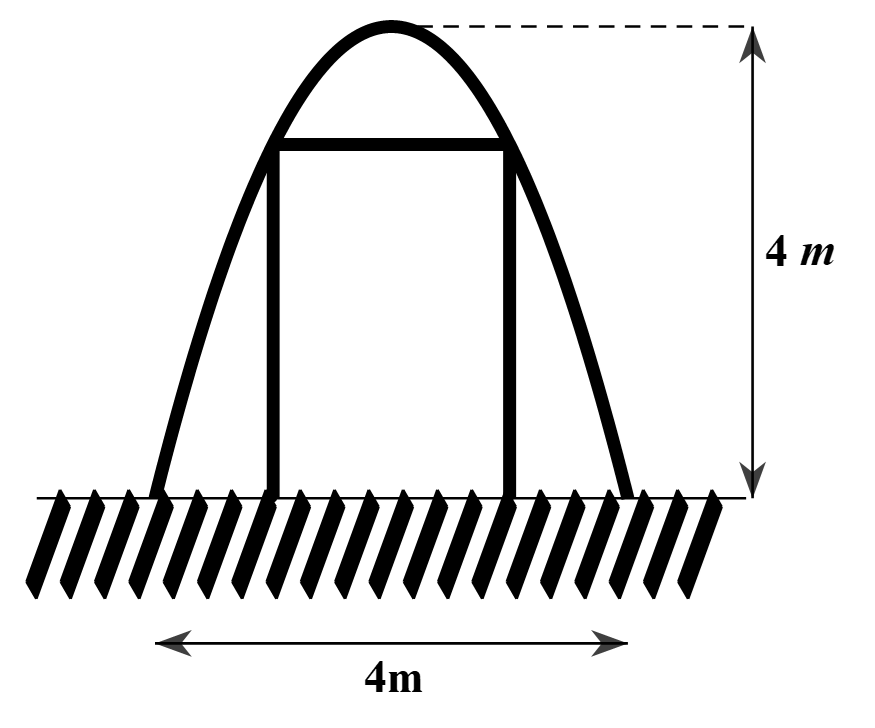
Đặt hệ tọa độ như hình vẽ, coi khung sắt là hình chữ nhật \[ABCD\]. Khi đó \[\left( P \right){\rm{ }}\]đi qua các điểm \[O\left( {0;0} \right)\]; \[\left( { - 2; - 4} \right)\]; \[\left( {2; - 4} \right)\] nên parabol \[\left( P \right)\] có phương trình: \[y = - {x^2}\].
Giả sử \[C \in \left( P \right)\]\[ \Rightarrow \] \[\left( {0 < x < 2} \right)\]. Khi đó \(BC = 2x\); suy ra
Ta có:
Suy ra \[{S^2} \le \frac{{1024}}{{27}}\] hay \[S \le \frac{{32\sqrt 3 }}{9}\]. Dấu xảy ra khi \[x = \frac{{2\sqrt 3 }}{3}\].
Vậy kích thước của khung thép có chiều rộng là \[\frac{{4\sqrt 3 }}{3}\,\,\left( {\rm{m}} \right)\]; chiều dài là \[\frac{8}{3}\,\,\left( {\rm{m}} \right)\].
Lời giải
Nếu thuê theo gói cố định thì hàng tháng anh Tâm phải trả số tiền là \(350000\) (đồng).
Nếu thuê theo gói linh hoạt thì hàng tháng anh Tâm phải trả số tiền là
\(189000 + 374.400 = 338600\) (đồng)
Như vậy, nếu anh Tâm nên thuê pin theo gói linh hoạt thì tiết kiệm hơn.
Số tiền anh Tâm tiết kiệm được mỗi tháng là \(350000 - 338600 = 11400\) (đồng).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.