(4,0 điểm).
Một trục lăn sơn nước có dạng một hình trụ. Đường kính của đường tròn đáy trục lăn là \(5{\rm{\;cm}}\), chiều dài trục lăn là \(23{\rm{\;cm}}\) (hình bên). Sau khi lăn trục lăn trọn \(15\) vòng trên một bức tường phẳng thì diện tích phủ sơn là bao nhiêu \({\rm{c}}{{\rm{m}}^2}\) (giả sử các đường lăn không chồng lấn lên nhau, lấy \(\pi = 3,14)\).
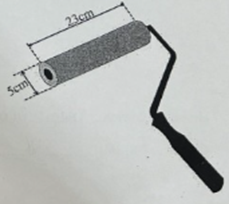
Một trục lăn sơn nước có dạng một hình trụ. Đường kính của đường tròn đáy trục lăn là \(5{\rm{\;cm}}\), chiều dài trục lăn là \(23{\rm{\;cm}}\) (hình bên). Sau khi lăn trục lăn trọn \(15\) vòng trên một bức tường phẳng thì diện tích phủ sơn là bao nhiêu \({\rm{c}}{{\rm{m}}^2}\) (giả sử các đường lăn không chồng lấn lên nhau, lấy \(\pi = 3,14)\).
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 41 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Trục lăn sơn có dạng hình trụ nên ta có:
Diện tích xung quanh trục lăn sơn là: \({S_{{\rm{mq\;}}}} = 2\pi rh\)\( = 2\pi .2,5.23\)\( = 361,1\,\,\left( {{\rm{\;c}}{{\rm{m}}^2}} \right)\)
Sau khi lăn 15 vòng trên một bức tường phẳng thì diện tích phủ sơn là: \(361,1.15 = 5416,5\left( {{\rm{\;c}}{{\rm{m}}^2}} \right)\).
Câu hỏi cùng đoạn
Câu 2:
Cho tam giác \(ABC\) nhọn. Đường tròn \(\left( O \right)\) đường kính \(BC\) cắt \(AB\), \(AC\) lần lượt tại \(E\) và \(D\); \(BD\) cắt \(CE\) tại \(H\), \(AH\) cắt \(BC\) tại \(I\). Từ \(A\) kẻ tiếp tuyến \(AM\), \(AN\) của đường tròn \(\left( O \right)\) (\(M\), \(N\) là tiếp điểm).
a) Chứng minh tứ giác \(AEHD\) nội tiếp.
b) Chứng minh \(AB.BE = BI.BC\), từ đó suy ra \(AB.BE + AC.CD = B{C^2}\).
c) Chứng minh ba điểm \(M\), \(H\), \(N\) thẳng hàng.
Cho tam giác \(ABC\) nhọn. Đường tròn \(\left( O \right)\) đường kính \(BC\) cắt \(AB\), \(AC\) lần lượt tại \(E\) và \(D\); \(BD\) cắt \(CE\) tại \(H\), \(AH\) cắt \(BC\) tại \(I\). Từ \(A\) kẻ tiếp tuyến \(AM\), \(AN\) của đường tròn \(\left( O \right)\) (\(M\), \(N\) là tiếp điểm).
a) Chứng minh tứ giác \(AEHD\) nội tiếp.
b) Chứng minh \(AB.BE = BI.BC\), từ đó suy ra \(AB.BE + AC.CD = B{C^2}\).
c) Chứng minh ba điểm \(M\), \(H\), \(N\) thẳng hàng.
Giải bởi Vietjack
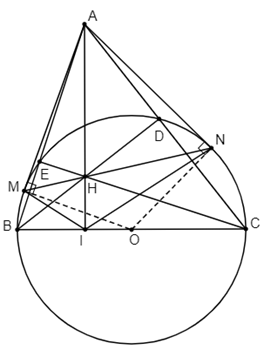
a) Vì \(\widehat {BEC}\) và \(\widehat {BDC}\) là hai góc nội tiếp chắn nửa đường tròn \(\left( O \right)\) nên: \(\widehat {BEC} = \widehat {BDC} = 90^\circ \), suy ra \(\widehat {AEH} = \widehat {ADH} = 90^\circ \)
Suy ra hai điểm \(E\) và \(D\) cùng thuộc đường tròn đường kính \(AH\)
Do đó bốn điểm \(A\), \(E\), \(H\), \(D\) cùng thuộc đường tròn đường kính \(AH\)
Vậy tứ giác \(AEHD\) nội tiếp đường tròn đường kính \(AH\)
b) Chứng minh \(H\) là trực tâm của \(\Delta ABC\) suy ra \(AI \bot BC\)
Chứng minh được (g.g)
Suy ra: \(\frac{{AB}}{{CB}} = \frac{{BI}}{{BE}}\) hay \(AB.BE = AI.BC\) (1)
Tương tự: \(AC.CD = AI.BC\) (2)
Từ (1) và (2) suy ra: \(AB.BE + AC.CD = BI.BC + CI.BC = \left( {BI + CI} \right).BC = B{C^2}\)
Vậy \(AB.BE + AC.CD = B{C^2}\)
c) Chứng minh 5 điểm \(A\,,\,M\,,\,I\,,\,O\,,\,N\) cùng thuộc đường tròn đường kính \(AO\), suy ra tứ giác \(AMIN\) nội tiếp , suy ra \(\widehat {AMI} + \widehat {ANI} = 180^\circ \) (*)
Chứng minh (g.g), suy ra \(\frac{{AE}}{{AI}} = \frac{{AH}}{{AB}}\) hay \(AE.AB = AI.AH\) (3)
Chứng minh (g.g), suy ra \(\frac{{AE}}{{AM}} = \frac{{AM}}{{AB}}\) hay \(AB.AE = A{M^2}\) (4)
Từ (3) và (4) suy ra hay \(\frac{{AM}}{{AI}} = \frac{{AH}}{{AM}}\)
Chứng minh (c.g.c), suy ra \(\widehat {AMI} = \widehat {AHM}\) (**)
Tương tự: \(\widehat {ANI} = \widehat {AHN}\) (***)
Từ (*), (**) và (***) suy ra \(\widehat {AHM} + \widehat {AHN} = 180^\circ \)
Vậy ba điểm \(M\), \(H\), \(N\) thẳng hàng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Nhóm có tần số lớn nhất là nhóm \[\left[ {600\,;\,750} \right)\] với tần số \[40\].
Tần số tương đối của nhóm có tần số lớn nhất là \[\frac{{40.100}}{{150}}\% = 26,7\% \].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
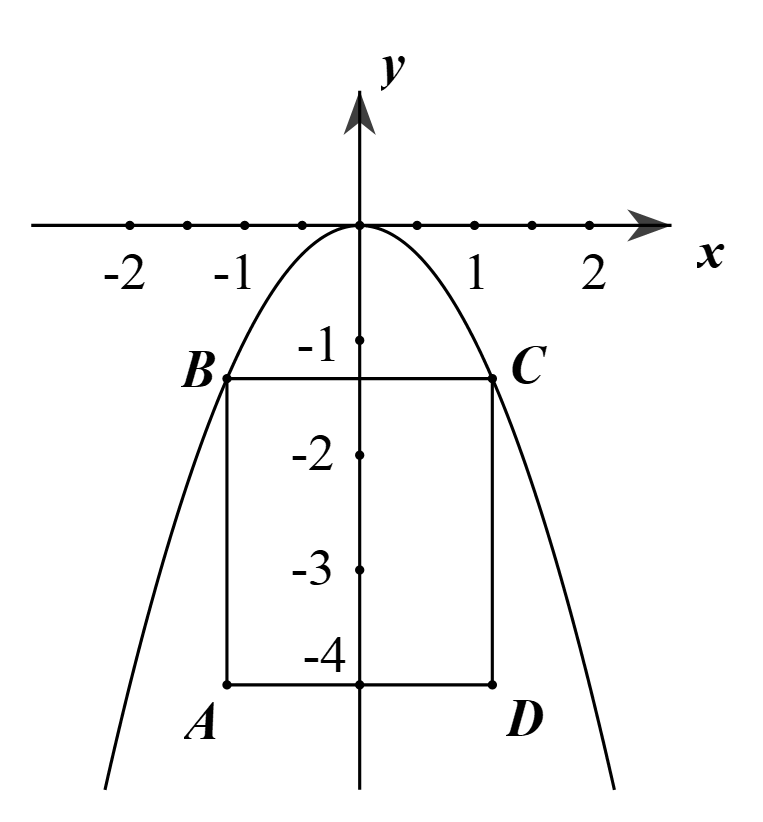
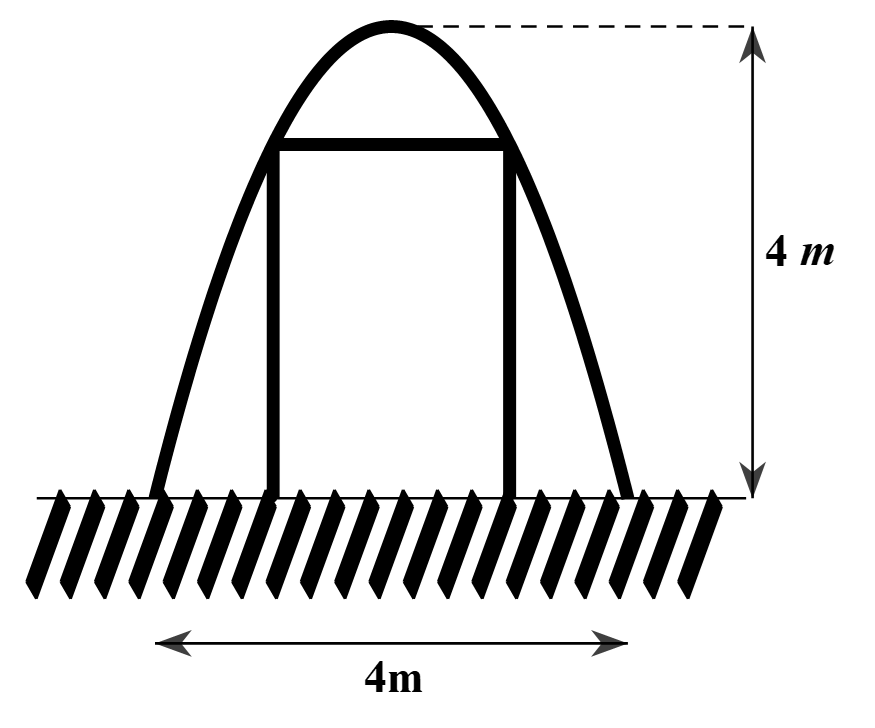
Đặt hệ tọa độ như hình vẽ, coi khung sắt là hình chữ nhật \[ABCD\]. Khi đó \[\left( P \right){\rm{ }}\]đi qua các điểm \[O\left( {0;0} \right)\]; \[\left( { - 2; - 4} \right)\]; \[\left( {2; - 4} \right)\] nên parabol \[\left( P \right)\] có phương trình: \[y = - {x^2}\].
Giả sử \[C \in \left( P \right)\]\[ \Rightarrow \] \[\left( {0 < x < 2} \right)\]. Khi đó \(BC = 2x\); suy ra
Ta có:
Suy ra \[{S^2} \le \frac{{1024}}{{27}}\] hay \[S \le \frac{{32\sqrt 3 }}{9}\]. Dấu xảy ra khi \[x = \frac{{2\sqrt 3 }}{3}\].
Vậy kích thước của khung thép có chiều rộng là \[\frac{{4\sqrt 3 }}{3}\,\,\left( {\rm{m}} \right)\]; chiều dài là \[\frac{8}{3}\,\,\left( {\rm{m}} \right)\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập