Cho đường tròn tâm \((O)\), đường kính \(AB = 2R\). Trên đường tròn \((O)\), lấy điểm \(C\) bất kì (\(C\) không trùng với \(A\) và \(B\)). Tiếp tuyến của đường tròn \((O)\) tại \(A\) cắt tia \(BC\) ở điểm \(D.\) Gọi \(H\) là hình chiếu của \(A\) trên đường thẳng \(DO.\) Tia \(AH\) cắt đường tròn \((O)\)tại điểm \(F\) (không trùng với \(A\)).
a) Chứng minh tứ giác \(AHCD\) nội tiếp được một đường tròn.
b) Chứng minh \[\Delta CFH\] là tam giác vuông.
c) Tính giá trị của biểu thức \(S = \frac{{BH.BC}}{{BF}}\).
Cho đường tròn tâm \((O)\), đường kính \(AB = 2R\). Trên đường tròn \((O)\), lấy điểm \(C\) bất kì (\(C\) không trùng với \(A\) và \(B\)). Tiếp tuyến của đường tròn \((O)\) tại \(A\) cắt tia \(BC\) ở điểm \(D.\) Gọi \(H\) là hình chiếu của \(A\) trên đường thẳng \(DO.\) Tia \(AH\) cắt đường tròn \((O)\)tại điểm \(F\) (không trùng với \(A\)).
a) Chứng minh tứ giác \(AHCD\) nội tiếp được một đường tròn.
b) Chứng minh \[\Delta CFH\] là tam giác vuông.
c) Tính giá trị của biểu thức \(S = \frac{{BH.BC}}{{BF}}\).
Quảng cáo
Trả lời:
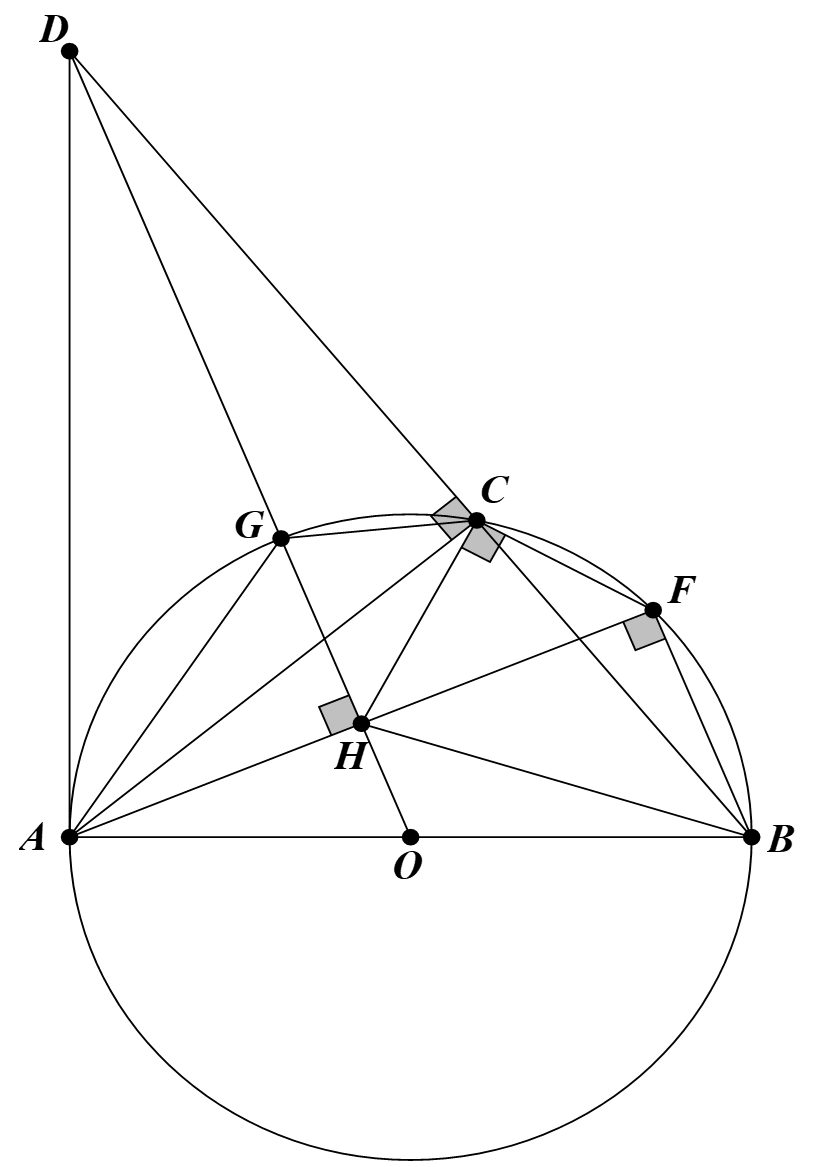
a) Do \(AH \bot DH\) \[ \Rightarrow \widehat {AHD} = 90^\circ \] nên A, H, D thuộc đường tròn đường kính AD (1)
Lại có \(\widehat {ACB} = {90^0}\)(góc nội tiếp chắn nửa đưởng tròn).
Suy ra \(\widehat {ACD} = {90^0}\) nên A, C, D thuộc đường tròn đường kính AD (1)
Từ (1) và (2) \( \Rightarrow \) A, H, C, D thuộc đường tròn đường kính AD hay tứ giác AHCD nội tiếp được một đường tròn.
b) Tứ giác AHCD nội tiếp \( \Rightarrow \widehat {HCB} = \widehat {DAH}\)
Ta có \(\widehat {BCF};\widehat {BAF}\) nội tiếp (O) cùng chắn \( \Rightarrow \widehat {BCF} = \widehat {BAF}\)
\( \Rightarrow \widehat {HCF} = \widehat {HCB} + \widehat {BCF} = \widehat {DAH} + \widehat {BAF} = \widehat {DAB} = 90^\circ .\)
Vậy \[\Delta CFH\] là tam giác vuông tại C.
c) Ta có: \[\widehat {FCB} = \widehat {HAB}\] (3) (hai góc nội tiếp cùng chắn cung ).
Tam giác OAD vuông tại A. Khi đó \[O{A^2} = OH.OD\]
Mà OA = OB nên \[O{B^2} = OH.OD \Rightarrow \frac{{OH}}{{OB}} = \frac{{OB}}{{OD}}\]
Suy ra hai tam giác OHB và OBD đồng dạng.
Suy ra \[\widehat {OBH} = \widehat {ODB}\] (4)
Ta lại có tứ giác AHCD nội tiếp nên \[\widehat {ODB} = \widehat {CAH}\] (5)
Tứ giác ABFC nội tiếp nên \[\widehat {CAH} = \widehat {CBF}\] (6)
Từ (4), (5) và (6) suy ra \[\widehat {OBH} = \widehat {CBF}\] (7)
Từ (3) và (7) suy ra hai tam giác HAB và FCB đồng dạng
Khi đó, ta có: \[\frac{{BC}}{{BA}} = \frac{{BF}}{{BH}} \Rightarrow \frac{{BC.BH}}{{BF}} = BA \Rightarrow \frac{{BC.BH}}{{BF}} = 2R\].
Vậy \[S = \frac{{BC.BH}}{{BF}} = 2R\].
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \[x\] (quyển) là số vở mà Thanh có thể mua. Theo bài ta có bất phương trình
\[\begin{array}{l}17x + 18 \le 100\\\,\,\,\,\,\,\,\,\,\,17x \le 100 - 18\\\,\,\,\,\,\,\,\,\,\,\,\,17\,x \le 82\\\,\,\,\,\,\,\,\,\,\,\,\,\,x \le \frac{{82}}{{17}}\end{array}\]
Vì số vở là số tự nhiên nên Thanh có thể mua nhiều nhất \[4\] quyển vở
Lời giải
Bảng tần số ghép nhóm
|
Chỉ số HDI |
\(\left[ {0;\,0,55} \right)\) |
\(\left[ {0,55;\,0,7} \right)\) |
\(\left[ {0,7;\,0,8} \right)\) |
\(\left[ {0,8;\,1} \right)\) |
Cộng |
|
Tần số |
0 |
5 |
2 |
4 |
\(N = 11\) |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.