(4,0 điểm)
Một khối gỗ dạng hình trụ, bán kính đường tròn đáy \[r = 10\left( {cm} \right),\]chiều cao \[h = 20(cm)\]. Người ta khoét rỗng hai nửa hình cầu như hình vẽ.
a. Tính thể tích của khối gỗ khi chưa khoét.
b. Hãy tính diện tích bề mặt của khối gỗ còn lại sau khi khoét (diện tích cả ngoài lẫn trong).
( các kết quả làm tròn đến hàng đơn vị)
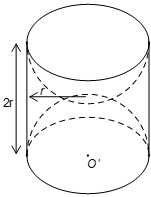
Một khối gỗ dạng hình trụ, bán kính đường tròn đáy \[r = 10\left( {cm} \right),\]chiều cao \[h = 20(cm)\]. Người ta khoét rỗng hai nửa hình cầu như hình vẽ.
a. Tính thể tích của khối gỗ khi chưa khoét.
b. Hãy tính diện tích bề mặt của khối gỗ còn lại sau khi khoét (diện tích cả ngoài lẫn trong).
( các kết quả làm tròn đến hàng đơn vị)

Quảng cáo
Trả lời:
a. Thể tích của khối gỗ lúc chưa khoét là:
\(V = \pi {r^2}h = \pi {.10^2}.20 \approx 6283\left( {c{m^3}} \right)\)
b. Diện tích bề mặt của khối gỗ còn lại gồm diện tích xung quanh của hình trụ (có bán kính đáy là \[r = 10\left( {cm} \right),\]và chiều cao \[h = 20(cm)\]) và diện tích hai nửa mặt cầu bán kính \[r = 10\left( {cm} \right),\]
Diện tích cần tìm là: \[S = 2\pi r.h + 4\pi {r^2} = 2\pi .10.20 + 4.\pi {.10^2} \approx 2513\left( {c{m^2}} \right)\]
Câu hỏi cùng đoạn
Câu 2:
Tứ giác \[ABCD\] nội tiếp đường tròn tâm \[O\] đường kính \[AD.\] Hai đường chéo \[AC,BD\] cắt nhau tại \[E.\] Từ \[E\] kẻ \[EF\]vuông góc với \[AD\] ( \[F \in AD\]). Đường thẳng \[CF\] cắt đường tròn tại điểm thứ hai là \[M.\] Giao điểm của \[BD\] và \[CF\] là \[N.\]Chứng minh :
a) \[CEFD\] là tứ giác nội tiếp.
b) \[FA\] là tia phân giác của \[\widehat {BFM}\] .
c) \[BE.DN = EN.BD\].
Tứ giác \[ABCD\] nội tiếp đường tròn tâm \[O\] đường kính \[AD.\] Hai đường chéo \[AC,BD\] cắt nhau tại \[E.\] Từ \[E\] kẻ \[EF\]vuông góc với \[AD\] ( \[F \in AD\]). Đường thẳng \[CF\] cắt đường tròn tại điểm thứ hai là \[M.\] Giao điểm của \[BD\] và \[CF\] là \[N.\]Chứng minh :
a) \[CEFD\] là tứ giác nội tiếp.
b) \[FA\] là tia phân giác của \[\widehat {BFM}\] .
c) \[BE.DN = EN.BD\].
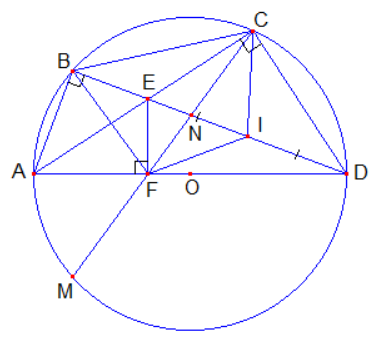
a) \[CEFD\] là tứ giác nội tiếp.
Ta có \(\widehat {ACD} = 90^\circ \) ( góc nội tiếp chắn nửa đường tròn)
Nên vuông tại \[C\]
Gọi \[I\] là trung điểm của \[ED\]
Ta có \[CI\] là đường trung tuyến hạ xuống cạnh huyền \[ED\]
Nên \[CI = IE = ID = \frac{1}{2}ED\] (1)
Tương tự trong tam giác \[EFD\] vuông tại \[F\], ta có
\[FI = IE = ID = \frac{1}{2}ED\] (2)
Từ (1) và (2) suy ra \[CI = FI = IE = ID\]
Hay tứ giác \[CEFD\] là tứ giác nội tiếp đường tròn tâm \[I\] đường kính \[ED\]
-----------------------------
b) \[FA\] là tia phân giác của \[\widehat {BFM}\]
Ta có \[CEFD\] nội tiếp=> \[\widehat {CED} = \widehat {CFD}\] ( hai góc nội tiếp cùng chắn )
Chứng minh tương tự câu a) ta có \[ABEF\] là tứ giác nội tiếp
=> \[\widehat {BEA} = \widehat {BFA}\] ( hai góc nội tiếp cùng chắn cung )
Mà \[\widehat {BEA} = \widehat {CED}\] ( đối đỉnh)
\[\widehat {AFM} = \widehat {CFD}\] ( đối đỉnh)
Do đó \[\widehat {BFA} = \widehat {AFM}\]
Hay \[FA\] là tia phân giác \[\widehat {BFM}\]
c) \[BE.DN = EN.BD\].
Ta có \[\widehat {EFC} = \widehat {EDC}\] ( hai góc nội tiếp cùng chắn )
\[\widehat {EFB} = \widehat {BAE}\] ( hai góc nội tiếp cùng chắn )
Mà \[\widehat {BAE} = \widehat {BAC} = \widehat {BDC} = \widehat {EDC}\] ( hai góc nội tiếp cùng chắn )
Suy ra \[\widehat {EFC} = \widehat {EFB}\] hay \[FE\] là tia phân giác của \[\widehat {BFC}\]
Trong có \[FE\] là phân giác trong tại đỉnh \[F\] \( \Rightarrow \frac{{BE}}{{EN}} = \frac{{FB}}{{FN}}\)
Mà\[EF \bot \;FD\] \[ \Rightarrow FD\] là phân giác ngoài tại đỉnh \[F\]\( \Rightarrow \frac{{BD}}{{DN}} = \frac{{FB}}{{FN}}\)
Suy ra \[\frac{{BE}}{{EN}} = \frac{{BD}}{{DN}} \Rightarrow BE.DN = EN.BD\]
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi số tiền bác Tuấn đã vay ngân hàng Sacombank và Vietcombank lần lượt là \[x,\]\[y\](tỉ đồng)
Điều kiện: \[0 < x < 5;\,\]\[0 < y < 5.\]
Theo bài, tổng số tiền vay là 5 tỉ đồng nên ta có phương trình:\[x + y = 5\].
Số tiền lãi phải trả mỗi năm cho ngân hàng Sacombank là \[x.12\% = 0,12x\](tỉ đồng).
Số tiền lãi phải trả mỗi năm cho ngân hàng Vietcombank là \[y.11\% = 0,11y\](tỉ đồng).
Theo bài, tổng số tiền lãi phải trả là 570 triệu đồng nên ta có phương trình:
\[0,12x + 0,11y = 0,57\]hay \[12x + 11y = 57.\]
Ta có hệ phương trình: \[\left\{ {\begin{array}{*{20}{l}}{x + y = 5}\\{12x + 11y = 57.}\end{array}} \right.\].
Nhân hai vế của phương trình thứ nhất với 11, ta được hệ phương trình: \[\left\{ {\begin{array}{*{20}{l}}{11x + 11y = 55}\\{12x + 11y = 57}\end{array}} \right.\].
Trừ hai vế của hai phương trình trên, ta được: \[x = 2\].
Thay \[x = 2\] vào phương trình \[x + y = 5\] ,
Ta được \[2 + y = 5\].
\[y = 3.\]
Ta thấy \[x = 2\] và \[y = 3.\] thỏa mãn điều kiện.
Vậy số tiền bác Tuấn đã vay của ngân hàng Sacombank là 2 tỉ đồng và Vietcombank là 3 tỉ đồng.
Lời giải
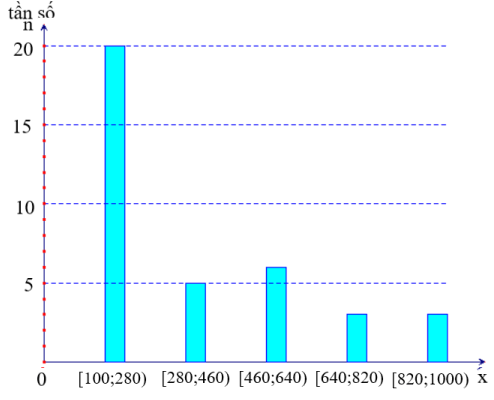
a) Tần số ghép nhóm của nhóm \[{\rm{[}}460;640)\]là 6.
b .Tần số tương đối ghép nhóm của nhóm \[{\rm{[10}}0;280)\]là \[f = \frac{{20}}{{37}}.100\% \approx 54\% \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.