(2,5 điểm)
Có hai loại quặng chứa \[75\% \] sắt và \[50\% \] sắt. Tính khối lượng của mỗi loại quặng đem trộn để được \[25\] tấn quặng chứa \[66\% \] sắt
(2,5 điểm)
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 12 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi khối lượng quặng chứa \[75\% \] sắt và \[50\% \] sắt là \[x,y\](tấn, \[x,y > 0\])
Theo bài ra ta có hệ phương trình \[\left\{ \begin{array}{l}x + y = 25\\\frac{{75x}}{{100}} + \frac{{50y}}{{100}} = \frac{{66}}{{100}}.25\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 16\\y = 9\end{array} \right.\](thỏa mãn điều kiện)
Vậy đem \[16\] tấn loại quặng chứa \[75\% \] sắt, \[9\] tấn loại quặng chứa \[50\% \] sắtCâu hỏi cùng đoạn
Câu 2:
Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình :
Hai công nhân làm chung một công việc thì sau \(5\) giờ \(50\) phút sẽ hoàn thành xong công việc. Sau khi làm chung \(5\) giờ thì người thứ nhất đi làm việc khác trong khi người thứ hai vẫn tiếp tục làm trong \(2\) giờ nữa mới hoàn thành xong công việc. Hỏi nếu làm riêng thì mỗi người phải mất bao nhiêu thời gian để hoàn thành xong công việc?
Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình :
Hai công nhân làm chung một công việc thì sau \(5\) giờ \(50\) phút sẽ hoàn thành xong công việc. Sau khi làm chung \(5\) giờ thì người thứ nhất đi làm việc khác trong khi người thứ hai vẫn tiếp tục làm trong \(2\) giờ nữa mới hoàn thành xong công việc. Hỏi nếu làm riêng thì mỗi người phải mất bao nhiêu thời gian để hoàn thành xong công việc?
Giải bởi Vietjack
|
Đổi \[5h50' = \frac{{35}}{6}h.\] Gọi thời gian công nhân thứ nhất làm một mình xong công việc là \(x\) (đơn vị: giờ, \(x > 0\)) |
|
Thời gian công nhân thứ hai làm một mình xong công việc là \(y\)(đơn vị: giờ, \(y > 0\)) |
|
Trong một giờ công nhân thứ nhất làm được \[\frac{1}{x}\] (công việc) Trong một giờ công nhân thứ nhất làm được \[\frac{1}{y}\] (công việc) |
|
Vì hai công nhân làm chung công việc đó sau \[\frac{{35}}{6}h\]thì xong nên ta có phương trình \[\frac{1}{x} + \frac{1}{y} = \frac{6}{{35}}\] (1) |
|
Vì Sau khi làm chung 5 giờ thì người thứ nhất đi làm việc khác trong khi người thứ hai vẫn tiếp tục làm trong 2 giờ nữa mới hoàn thành xong công việc nên ta có phương trình \[\frac{5}{x} + \frac{7}{y} = 1\] (2) |
|
Từ (1) và (2) ta có hệ \[\left\{ \begin{array}{l}\frac{1}{x} + \frac{1}{y} = \frac{6}{{35}}\\\frac{5}{x} + \frac{7}{y} = 1\end{array} \right.\] |
|
Giải hệ tìm được \[\left\{ \begin{array}{l}x = 10\\y = 14\end{array} \right..\] (tmđk) |
|
Vậy công nhân thứ nhất làm một mình xong công việc trong \[10\] giờ, công nhân thứ hai làm một mình xong công việc trong \[14\] giờ. |
Câu 3:
Cho phương trình \(3{x^2} - 11x - 15 = 0\) có 2 nghiệm là \({x_1},{x_2}\) Không giải phương trình, hãy tính giá trị của biểu thức \(A = \frac{{3{x_1}}}{{{x_2}}} + \frac{{3{x_2}}}{{{x_1}}}\)
Giải bởi Vietjack
Ta có
\(\begin{array}{l}3{x_1} + 4{x_2} = 3\\ \Leftrightarrow ({x_1} + {x_2}) + {x_2} = 6\\ \Rightarrow {x_2} = - 9\end{array}\)
Vì \[x = - 9\] là nghiệm của phương trình nên ta có \({\left( { - 9} \right)^2} - 5.\left( { - 9} \right) + m + 4 = 0\).
Tìm được \(m = - 3 \pm \sqrt {13} \)Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
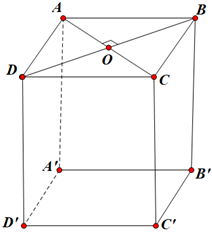
Ta đặt \[AC = 2m;BD = 2n.\]
Diện tích đáy \[ABCD\] là: \[S = \frac{1}{2}.2m.2n = 2mn.\]
Mặt khác: \[S = \frac{V}{h} = \frac{{1280}}{{20}} = 64\left( {c{m^2}} \right)\]
Vậy \[2m.n = 64\left( {c{m^2}} \right).\]
Vậy \[{S_{xq}}\] nhỏ nhất khi \[AB\] nhỏ nhất.
Mặt khác \[{m^2} + {n^2} \ge 2mn\]. Do đó \[A{B^2} \ge 64 \Rightarrow
Diện tích xung quanh hình lăng trụ đứng là:
\[{S_{xq}} = 4.AB.20 = 80AB.\]
Gọi \[O\] là giao điểm của hai đường chéo \[AC\] và \[BD\]. Ta có \[AC \bot BD\] tại \[O\].
Xét \[\Delta AOB\] vuông tại \[O\], ta có: \[A{B^2} = O{A^2} + O{B^2} = {m^2} + {n^2}.\]
Mặt khác \[{m^2} + {n^2} \ge 2mn\]. Do đó \[A{B^2} \ge 64 \Rightarrow
AB \ge 8\left( {cm} \right).\]
Vậy giá trị nhỏ nhất của \[AB\] là \[8cm\] khi \[m = n\] tức là khi \[ABCD\] là hình vuông.
Giá trị nhỏ nhất của diện tích xung quanh là \[4.8.20 = 640\left( {c{m^2}} \right).\]
Lời giải
a) Bảng tần số tương đối:
|
Số đại biểu |
\[84\] |
\[64\] |
\[64\] |
\[16\]16 |
12 |
|
Tần số tương đối |
\[42\% \] |
\[32\% \] |
\[12\% \] |
\[8\% \] |
\[6\% \] |
b) Tỉ lệ phần trăm đại biểu sử dụng được ít nhất 2 ngoại ngữ là: \[32\% {\rm{ }} + {\rm{ }}12\% {\rm{ }} + {\rm{ }}8\% {\rm{ }} + {\rm{ }}6\% {\rm{ }} = {\rm{ }}58\% .\]
c) Ý kiến đó đúng vì:
- Tỉ lệ đại biểu sử dụng được 3 ngôn ngữ của 1 năm trước là: \(\frac{{54}}{{220}}.100\% = 24,5\% \).
- Tỉ lệ đại biểu sử dụng được 3 ngôn ngữ của nay là: .\[12\% {\rm{ }} + {\rm{ }}8\% {\rm{ }} + {\rm{ }}6\% {\rm{ }} = {\rm{ }}26\% {\rm{ }} > {\rm{ }}24,5\% \]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập