(4,0 điểm)
Đường ống nối hai bể cá trong một thủy cung có dạng một hình trụ, độ dài của đường ống là \[30m.\] Dung tích của đường ống nói trên là \[1800{\rm{ }}{m^3}.\] Tính diện tích đáy của đường ống.
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 12 !!
Quảng cáo
Trả lời:
Câu hỏi cùng đoạn
Câu 2:
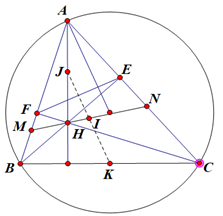
Cho tam giác \(ABC\) nhọn \(\left( {AB < AC} \right)\) nội tiếp đường tròn \((O).\) Hai đường cao \(BE\) và \(CF\) của tam giác \(ABC\) cắt nhau tại điểm \(H.\) Gọi \[K\] là trung điểm \[BC.\]
a) Chứng minh \(\Delta AEF\) đồng dạng \(\Delta ABC.\)
b) Chứng minh đường thẳng \(OA\) vuông góc với đường thẳng \[EF.\]
c) Đường phân giác góc \(FHB\) cắt \(AB\) và \(AC\) lần lượt tại \(M\) và \(N.\;\)Gọi \(I\)là trung điểm của \(MN,\,J\)là trung điểm của\(AH.\) Chứng minh tứ giác \(AFHI\)nội tiếp và ba điểm\(I,J,K\)thẳng hàng.
Cho tam giác \(ABC\) nhọn \(\left( {AB < AC} \right)\) nội tiếp đường tròn \((O).\) Hai đường cao \(BE\) và \(CF\) của tam giác \(ABC\) cắt nhau tại điểm \(H.\) Gọi \[K\] là trung điểm \[BC.\]
a) Chứng minh \(\Delta AEF\) đồng dạng \(\Delta ABC.\)
b) Chứng minh đường thẳng \(OA\) vuông góc với đường thẳng \[EF.\]
c) Đường phân giác góc \(FHB\) cắt \(AB\) và \(AC\) lần lượt tại \(M\) và \(N.\;\)Gọi \(I\)là trung điểm của \(MN,\,J\)là trung điểm của\(AH.\) Chứng minh tứ giác \(AFHI\)nội tiếp và ba điểm\(I,J,K\)thẳng hàng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
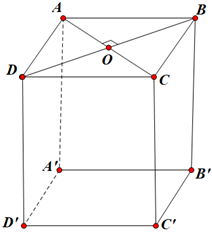
Ta đặt \[AC = 2m;BD = 2n.\]
Diện tích đáy \[ABCD\] là: \[S = \frac{1}{2}.2m.2n = 2mn.\]
Mặt khác: \[S = \frac{V}{h} = \frac{{1280}}{{20}} = 64\left( {c{m^2}} \right)\]
Diện tích xung quanh hình lăng trụ đứng là:
\[{S_{xq}} = 4.AB.20 = 80AB.\]
Gọi \[O\] là giao điểm của hai đường chéo \[AC\] và \[BD\]. Ta có \[AC \bot BD\] tại \[O\].
Xét \[\Delta AOB\] vuông tại \[O\], ta có: \[A{B^2} = O{A^2} + O{B^2} = {m^2} + {n^2}.\]
Mặt khác \[{m^2} + {n^2} \ge 2mn\]. Do đó \[A{B^2} \ge 64 \Rightarrow
AB \ge 8\left( {cm} \right).\]
Vậy giá trị nhỏ nhất của \[AB\] là \[8cm\] khi \[m = n\] tức là khi \[ABCD\] là hình vuông.
Lời giải
a) Bảng tần số tương đối:
|
Số đại biểu |
\[84\] |
\[64\] |
\[64\] |
\[16\]16 |
12 |
|
Tần số tương đối |
\[42\% \] |
\[32\% \] |
\[12\% \] |
\[8\% \] |
\[6\% \] |
b) Tỉ lệ phần trăm đại biểu sử dụng được ít nhất 2 ngoại ngữ là: \[32\% {\rm{ }} + {\rm{ }}12\% {\rm{ }} + {\rm{ }}8\% {\rm{ }} + {\rm{ }}6\% {\rm{ }} = {\rm{ }}58\% .\]
c) Ý kiến đó đúng vì:
- Tỉ lệ đại biểu sử dụng được 3 ngôn ngữ của 1 năm trước là: \(\frac{{54}}{{220}}.100\% = 24,5\% \).
- Tỉ lệ đại biểu sử dụng được 3 ngôn ngữ của nay là: .\[12\% {\rm{ }} + {\rm{ }}8\% {\rm{ }} + {\rm{ }}6\% {\rm{ }} = {\rm{ }}26\% {\rm{ }} > {\rm{ }}24,5\% \]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.