a.Tìm điều kiện của x để biểu thức \[A = \sqrt {x - 1} \] có nghĩa.
b)Không sử dụng máy tính cầm tay, tính giá trị của biểu thức \[B = \sqrt 9 - \sqrt 4 + \sqrt {16} \]
c)Rút gọn biểu thức \[C = \frac{x}{{x - 4}} + \frac{1}{{\sqrt x + 2}} - \frac{1}{{\sqrt x - 2}}\] với \[x \ge 0\] và \[x \ne 4\]
a.Tìm điều kiện của x để biểu thức \[A = \sqrt {x - 1} \] có nghĩa.
b)Không sử dụng máy tính cầm tay, tính giá trị của biểu thức \[B = \sqrt 9 - \sqrt 4 + \sqrt {16} \]
c)Rút gọn biểu thức \[C = \frac{x}{{x - 4}} + \frac{1}{{\sqrt x + 2}} - \frac{1}{{\sqrt x - 2}}\] với \[x \ge 0\] và \[x \ne 4\]
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Biểu thức\[A = \sqrt {x - 1} \] có nghĩa khi \[x - 1 \ge 0 \Leftrightarrow x \ge 1\]
b)\[\begin{array}{l}B = \sqrt 9 - \sqrt 4 + \sqrt {16} \\ \Leftrightarrow B = \sqrt {{3^2}} - \sqrt {{2^2}} + \sqrt {{4^2}} \\ \Leftrightarrow B = 3 - 2 + 4\\ \Leftrightarrow B = 5\end{array}\]
Vậy \[B = 5\]
c)\[\begin{array}{l}C = \frac{x}{{x - 4}} + \frac{1}{{\sqrt x + 2}} - \frac{1}{{\sqrt x - 2}}\\ \Leftrightarrow C = \frac{x}{{x - 4}} + \frac{{\sqrt x - 2}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}} - \frac{{\sqrt x + 2}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}}\\ \Leftrightarrow C = \frac{{x + \sqrt x - 2 - \sqrt x - 2}}{{x - 4}}\\ \Leftrightarrow C = \frac{{x - 4}}{{x - 4}} = 1\end{array}\]
Vậy \[C = 1\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a)Xét tứ giác \[AOED\], ta có: \[\widehat {OAD} = 90^\circ \] (tính chất tiếp tuyến )
\[\widehat {OED} = 90^\circ \]( giả thuyết )
\[ \Rightarrow \widehat {OAD} + \widehat {OED} = 90^\circ + 90^\circ = 180^\circ \]
Vậy tứ giác \[AOED\]nội tiếp đường tròn
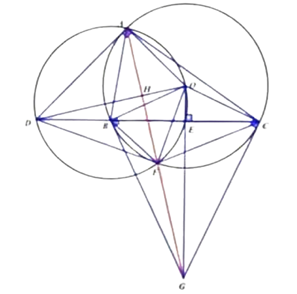
b)Ta có \[AOFD\] là tứ giác nội tiếp \[ \Rightarrow \widehat {OFD} = 90^\circ \]
Suy ra \[DF\] là tiếp tuyến của đường tròn \[\left( O \right)\]
Xét \[\Delta DFB\] và \[\Delta DCF\], ta có:
\[\widehat D\]:góc chung
\[\widehat {DFB} = \widehat {DCF}\] ( góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn )
Suy ra: \[\Delta DFB \sim \Delta DCF(g - g) \Rightarrow \frac{{DF}}{{DC}} = \frac{{FB}}{{FC}}\left( 1 \right)\]
Xét \[\Delta DAB\] và \[\Delta DCA\], ta có:
\[\widehat D\]:góc chung
\[\widehat {DAB} = \widehat {ACB}\] ( góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn )
Suy ra: \[\Delta DAB \sim \Delta DCA(g - g) \Rightarrow \frac{{DA}}{{DC}} = \frac{{AB}}{{AC}}\left( 2 \right)\]
Vì \[DF = DA\] ( tính chất 2 tiếp tuyến cắt nhau ) (3)
Từ (1), (2) và (3) suy ra \[\frac{{FB}}{{FC}} = \frac{{AB}}{{AC}}\]
c)Ta có: \[GC = GB\] (tính chất hai tiếp tuyến cắt nhau)
\[OC = OB\] (bán kính)
Nên \[OG\] là đường trung trực của \[BC\], suy ra \[OG \bot BC\]
Mặt khác: \[OE \bot BC\], nên ba điểm \[O,E,G\] thẳng hàng.
Ta có: \[OA = {\rm{OF; DA = DF}}\]; nên \[{\rm{OD}}\] là đường trung trực của \[{\rm{AF}}\]
Do đó \[{\rm{OD}} \bot {\rm{AF}}\] tại \[H\](5)
Tam giác \[OCG\] vuông tại \[C\] nên \[OE.OG = O{C^2}\]
Tam giác \[OAD\] vuông tại \[H\] nên \[O{A^2} = OH.OD\]
Mà \[OA = OC\] nên \[OE.OG = OH.OD\]. Suy ra \[EHDG\] là tứ giác nội tiếp.
Mà \[\widehat {GED} = 90^\circ \] nên \[\widehat {GHD} = 90^\circ \] (6)
Từ (5) và (6), suy ra \[A,F,G\] thẳng hàng.
Lời giải
\[{V_1} = \frac{1}{3}\pi .O{C^2}.OB = 800\pi \]
Khi quay tam giác \[OBC\] một vòng cạnh \[OC\] cố định thì
\[{V_2} = \frac{1}{3}\pi .O{B^2}.OC = 1920\pi \]
Ta có: \[\frac{{{V_1}}}{{{V_2}}} = \frac{{\frac{1}{3}\pi .O{C^2}.OB}}{{\frac{1}{3}\pi .O{B^2}.OC}} = \frac{{800\pi }}{{1920\pi }} \Leftrightarrow \frac{{OC}}{{OB}} = \frac{5}{{12}} \Rightarrow OC = \frac{5}{{12}}OB\]
Suy ra: \[{V_1} = \frac{1}{3}\pi .{\left( {\frac{5}{{12}}.OB} \right)^2}.OB = 800\pi \Rightarrow \frac{{25}}{{144}}.O{B^2} = 2400 \Rightarrow OB = 24(cm)\]
Do đó: \[OC = \frac{5}{{12}}.OB = \frac{5}{{12}}.24 = 10\left( {cm} \right)\]
Vậy độ dài của \[OB\] và \[OC\] lần lượt là \[24\left( {cm} \right)\] và \[10\left( {cm} \right)\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập