Phương tiện bạn Lan có thể chọn đi từ Phú Thọ xuống Hà Nội rồi từ Hà Nội vào Đà Nẵng được thể hiện qua sơ đồ hình cây sau:

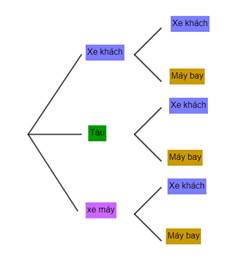
Hỏi bạn Lan có mấy cách chọn đi từ Phú Thọ vào Đà Nẵng mà qua Hà Nội?

Đáp án đúng là: A

Đường thẳng \(\Delta :x - y = 0\) có một vectơ pháp tuyến là \(\overrightarrow {{n_1}}  = \left( {1;\, - 1} \right)\) nên nó có một vectơ chỉ phương là \(\overrightarrow {{u_1}}  = \left( {1;\,\,1} \right)\).

Giả sử \(H\) là hình chiếu vuông góc của \(M\left( {1;\,\,2} \right)\) lên đường thẳng \(\Delta \), vì \(H \in \Delta \) nên \(H\left( {t;\,\,t} \right)\).

Vì \(MH \bot \Delta  \Rightarrow \overrightarrow {MH}  \bot \overrightarrow u  \Rightarrow \overrightarrow {MH} .\overrightarrow u  = 0 \Leftrightarrow t - 1 + t - 2 = 0 \Leftrightarrow t = \frac{3}{2}\).

Vậy \(H\left( {\frac{3}{2};\,\frac{3}{2}} \right)\).

Số cách chọn 4 học sinh bất kì từ 12 học sinh là \(C_{12}^4 = 495\) cách.

Số cách chọn 4 học sinh mà mỗi lớp có ít nhất một em được tính như sau:

\( * \) TH1: Lớp \(A\) có 2 học sinh, các lớp \(B,C\) mỗi lớp có 1 học sinh:

Chọn 2 học sinh trong 5 học sinh lớp \(A\) có \(C_5^2\) cách.

Chọn 1 học sinh trong 4 học sinh lớp \(B\) có \(C_4^1\) cách.

Chọn 1 học sinh trong 3 học sinh lớp \(C\) có \(C_3^1\) cách.

Suy ra số cách chọn là \(C_5^2.C_4^1.C_3^1 = 120\) cách.

\( * \) TH2: Lớp \(B\) có 2 học sinh, các lớp \(A,C\) mỗi lớp có 1 học sinh:

Tương tự ta có số cách chọn là \(C_5^1.C_4^2.C_3^1 = 90\) cách.

\( * \) TH3: Lớp \(C\) có 2 học sinh, các lớp \(A,B\) mỗi lớp có 1 học sinh:

Tương tự ta có số cách chọn là \(C_5^1.C_4^1.C_3^2 = 60\) cách.

Vậy số cách chọn 4 học sinh mà mỗi lớp có ít nhất một học sinh là \(120 + 90 + 60 = 270\) cách.

Số cách chọn ra 4 học sinh thuộc không quá 2 trong 3 lớp trên là \(495 - 270 = 225\) cách.