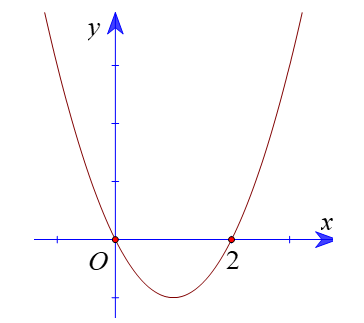
Cho đồ thị hàm số bậc hai \(y = f\left( x \right)\).
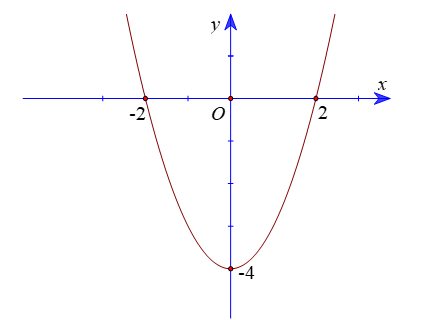
Cho đồ thị hàm số bậc hai \(y = f\left( x \right)\).

a) Tam thức bậc hai \(f\left( x \right)\) có bảng xét dấu:
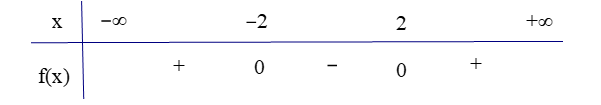
b) Bất phương trình \(f\left( x \right) < - 3\) có tập nghiệm là \(S = \left( { - 1;1} \right)\).
c) Phương trình \(\sqrt {f\left( x \right)} = \sqrt {{x^2} - 2x + 4} \) có 2 nghiệm phân biệt thuộc khoảng \(\left( { - 2;2} \right)\).
Quảng cáo
Trả lời:
a) Dựa vào đồ thị hàm số ta có bảng xét dấu

b)
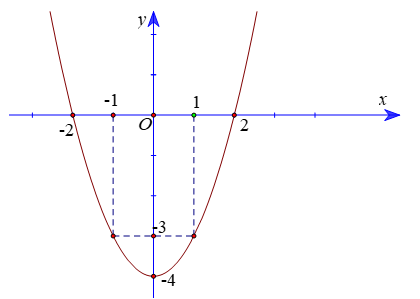
Dựa vào đồ thị hàm số ta có \(f\left( x \right) < - 3\)\( \Leftrightarrow - 1 < x < 1\).
Vậy bất phương trình \(f\left( x \right) < - 3\) có tập nghiệm là \(S = \left( { - 1;1} \right)\).
c) Gọi \(f\left( x \right) = a{x^2} + bx + c\left( {a > 0} \right)\).
Đồ thị hàm số đi qua các điểm \(\left( { - 2;0} \right);\left( {2;0} \right);\left( {0; - 4} \right)\) nên ta có hệ phương trình
\(\left\{ \begin{array}{l}4a - 2b + c = 0\\4a + 2b + c = 0\\c = - 4\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 0\\c = - 4\end{array} \right.\). Vậy \(f\left( x \right) = {x^2} - 4\).
Khi đó \(\sqrt {f\left( x \right)} = \sqrt {{x^2} - 2x + 4} \)\( \Leftrightarrow \sqrt {{x^2} - 4} = \sqrt {{x^2} - 2x + 4} \).
Bình phương hai vế của phương trình ta được \({x^2} - 4 = {x^2} - 2x + 4\)\( \Rightarrow 2x = 8 \Rightarrow x = 4\).
Thay \(x = 4\) vào phương trình ta thấy thỏa mãn.
Vậy phương trình có 1 nghiệm \(x = 4\).
d) \(\sqrt {f\left( x \right)} = x + 1\)\( \Leftrightarrow \sqrt {{x^2} - 4} = x + 1\).
Bình phương hai vế của phương trình ta được \({x^2} - 4 = {\left( {x + 1} \right)^2}\)\( \Rightarrow 2x = - 5 \Rightarrow x = - \frac{5}{2}\).
Thay \(x = - \frac{5}{2}\) vào phương trình ta thấy không thỏa mãn.
Vậy phương trình vô nghiệm.
Đáp án: a) Đúng; b) Đúng; c) Sai; d) Đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chi phí sản xuất cho \(x\) sản phẩm là \(C\left( x \right) = x \cdot G\left( x \right) = x\left( {\frac{{20}}{x} + 100} \right) = 20 + 100x\).
Khi đó lợi nhật là \(L\left( x \right) = - 20{x^2} + 2200x - 19980 - 20 - 100x = - 20{x^2} + 2100x - 20000\).
Để lợi nhuận đạt trên 20 triệu đồng thì \(L\left( x \right) > 20000\)\( \Leftrightarrow - 20{x^2} + 2100x - 20000 > 20000\)
\( \Leftrightarrow - 20{x^2} + 2100x - 40000 > 0\)\( \Leftrightarrow 25 < x < 80\).
Vậy doanh nghiệp cần sản xuất ít nhất 26 sản phẩm.
Câu 2
Lời giải
Dựa vào đồ thị ta có \(f\left( x \right) > 0\)\( \Leftrightarrow x \in \left( { - \infty ;0} \right) \cup \left( {2; + \infty } \right)\). Chọn A.
Câu 3
a) Khi \(m = 1\) thì \(f\left( x \right) < 0,\forall x \in \mathbb{R}\).
b) Khi \(m > 3\) thì \(f\left( x \right)\) có hai nghiệm trái dấu.
c) Khi \(m \in \left( { - 1;2} \right)\) thì tam thức có hai nghiệm phân biệt.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Nếu \(\Delta < 0\) thì \(f\left( x \right)\) luôn cùng dấu với hệ số \(b\), với mọi \(x \in \mathbb{R}\).
B. Nếu \(\Delta > 0\) thì \(f\left( x \right)\) luôn cùng dấu với hệ số \(a\), với mọi \(x \in \mathbb{R}\).
C. Nếu \(\Delta = 0\) thì \(f\left( x \right)\) luôn cùng dấu với hệ số \(a\), với mọi \(x \in \mathbb{R}\backslash \left\{ {\frac{{ - b}}{{2a}}} \right\}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.