Bạn Hà dự định làm một khung ảnh hình chữ nhật sao cho phần trong của khung là hình chữ nhật có kích thước \(6\;{\rm{cm}} \times 11\;{\rm{cm}}\), độ rộng viền xung quanh là \(x\left( {{\rm{cm}}} \right)\) (tham khảo hình vẽ). Diện tích của viền khung ảnh không vượt quá 38 cm2. Hỏi độ rộng viền khung ảnh lớn nhất là bao nhiêu cm?
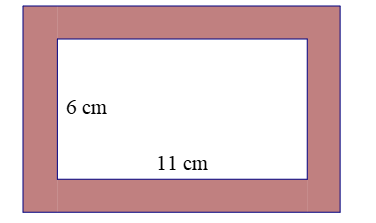
Bạn Hà dự định làm một khung ảnh hình chữ nhật sao cho phần trong của khung là hình chữ nhật có kích thước \(6\;{\rm{cm}} \times 11\;{\rm{cm}}\), độ rộng viền xung quanh là \(x\left( {{\rm{cm}}} \right)\) (tham khảo hình vẽ). Diện tích của viền khung ảnh không vượt quá 38 cm2. Hỏi độ rộng viền khung ảnh lớn nhất là bao nhiêu cm?

Quảng cáo
Trả lời:
Đáp án:
Chiều dài khung ảnh hình chữ nhật là \(11 + 2x\) (cm).
Chiều rộng khung ảnh hình chữ nhật là \(6 + 2x\) (cm).
Diện tích khung ảnh là \(\left( {11 + 2x} \right)\left( {6 + 2x} \right)\) (cm2).
Diện tích phần trong của khung ảnh là \(6 \cdot 11 = 66\) (cm2).
Diện tích viền của khung ảnh là \(\left( {11 + 2x} \right)\left( {6 + 2x} \right) - 66\).
Để diện tích viền không vượt quá 38 cm2 thì
\(\left( {11 + 2x} \right)\left( {6 + 2x} \right) - 66 \le 38\)\( \Leftrightarrow 4{x^2} + 34x - 38 \le 0\)\( \Leftrightarrow - \frac{{19}}{2} \le x \le 1\).
Vì \(x > 0\) nên \( \Leftrightarrow 0 < x \le 1\).
Vậy độ rộng của viền khung ảnh lớn nhất là 1 cm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chi phí sản xuất cho \(x\) sản phẩm là \(C\left( x \right) = x \cdot G\left( x \right) = x\left( {\frac{{20}}{x} + 100} \right) = 20 + 100x\).
Khi đó lợi nhật là \(L\left( x \right) = - 20{x^2} + 2200x - 19980 - 20 - 100x = - 20{x^2} + 2100x - 20000\).
Để lợi nhuận đạt trên 20 triệu đồng thì \(L\left( x \right) > 20000\)\( \Leftrightarrow - 20{x^2} + 2100x - 20000 > 20000\)
\( \Leftrightarrow - 20{x^2} + 2100x - 40000 > 0\)\( \Leftrightarrow 25 < x < 80\).
Vậy doanh nghiệp cần sản xuất ít nhất 26 sản phẩm.
Câu 2
Lời giải
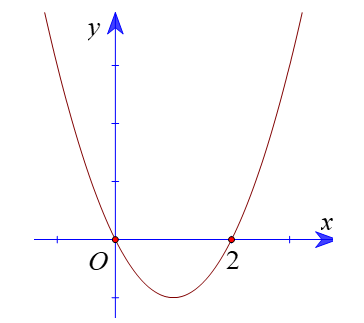
Dựa vào đồ thị ta có \(f\left( x \right) > 0\)\( \Leftrightarrow x \in \left( { - \infty ;0} \right) \cup \left( {2; + \infty } \right)\). Chọn A.
Câu 3
a) Khi \(m = 1\) thì \(f\left( x \right) < 0,\forall x \in \mathbb{R}\).
b) Khi \(m > 3\) thì \(f\left( x \right)\) có hai nghiệm trái dấu.
c) Khi \(m \in \left( { - 1;2} \right)\) thì tam thức có hai nghiệm phân biệt.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Nếu \(\Delta < 0\) thì \(f\left( x \right)\) luôn cùng dấu với hệ số \(b\), với mọi \(x \in \mathbb{R}\).
B. Nếu \(\Delta > 0\) thì \(f\left( x \right)\) luôn cùng dấu với hệ số \(a\), với mọi \(x \in \mathbb{R}\).
C. Nếu \(\Delta = 0\) thì \(f\left( x \right)\) luôn cùng dấu với hệ số \(a\), với mọi \(x \in \mathbb{R}\backslash \left\{ {\frac{{ - b}}{{2a}}} \right\}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.