(4,0 điểm)

1) Gia đình bạn Khánh đang sử dụng một thùng đựng nước dạng hình trụ với bán kính đáy bằng \(50\) cm và chiều cao bằng \(150\) cm. Thùng đựng nước được đặt thẳng đứng trên mặt sàn như hình vẽ minh họa bên. (Lấy \(\pi  \approx 3,14\) và coi chiều dài của thùng là không đáng kể).

a) Tính diện tích xung quanh của thùng đựng nước.

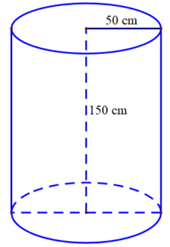
b) Sau một thời gian, gia đình bạn Khánh sử dụng nước trong thùng thì mực nước còn lại đã thấp hơn \(40\) cm so với mực nước ban đầu. Tính thể tích nước trong thùng mà gia đình bạn Khánh đã sử dụng trong khoảng thời gian đó.

 

Ta có hình vẽ của bài toán:

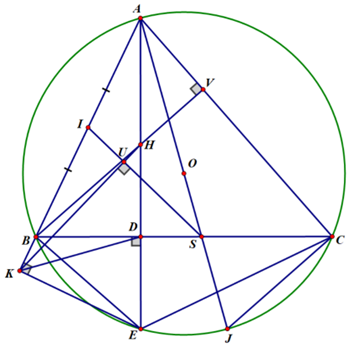
                a) Vì \(AD\) là đường cao của \(\Delta ABC\) nên \(AD \bot BC\) tại \(D\), mà \(E \in AD\)

                Suy ra: \(\widehat {ADB} = \widehat {ADC} = \widehat {BDE} = \widehat {CDE} = 90^\circ .\)

                Có \(EK \bot AB\) tại \(K\) nên \(\widehat {EKB} = \widehat {EKA} = 90^\circ .\)

                Ta có \(\widehat {EDB} = 90^\circ \) nên \(\Delta EDB\) vuông tại \(D\), suy ra \(\Delta EDB\) nội tiếp đường tròn đường kính \(BE\)

                Suy ra ba điểm \(D,B,E\) thuộc đường tròn đường kính \(BE\).     (1)

                Ta có \(\widehat {EKB} = 90^\circ  \Rightarrow \Delta EKB\) vuông tại \(K\), suy ra \(\Delta EKB\) nội tiếp đường tròn đường kính \(BE\)

                Suy ra ba điểm \(K,B,E\) thuộc đường tròn đường kính \(BE\).     (2)

                Từ (1) và (2) suy ra bốn điểm \(E,D,K,B\) cùng thuộc đường tròn đường kính \[BE\].

                2) Vì bốn điểm \(E,D,K,B\) cùng thuộc một đường tròn, nên tứ giác \(BDEK\) là tứ giác nội tiếp

                Suy ra \(\widehat {KED} + \widehat {KBD} = 180^\circ \) (tính chất), mà \(\widehat {ABC} + \widehat {KBD} = {180^{\rm{o}}}\) (hai góc kề bù) \( \Rightarrow \widehat {KED} = \widehat {ABC}\)

                Mà \(\widehat {AEC} = \widehat {ABC}\) (hai góc nội tiếp cùng chắn  của \(\left( O \right)\)) nên \(\widehat {KED} = \widehat {AEC}\).

                Vậy \(EA\) là tia phân giác của góc \(CEK\)

                *) Kéo dài \(AO\) cắt \(\left( O \right)\) tại điểm \(J \Rightarrow AJ\) là đường kính của \(\left( O \right) \Rightarrow \widehat {ACJ} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn).

                Xét \(\Delta ADB\) và \(\Delta ACJ\) có:

 \(\widehat {ABD} = \widehat {ABC} = \widehat {AJC}\) (hai góc nội tiếp cùng chắn  của \(\left( O \right)\))

 \(\widehat {ADB} = \widehat {ACJ} = 90^\circ \)

 (hai góc tương ứng) \( \Rightarrow \widehat {BAE} = \widehat {SAC}\).

                Ta có: \[\widehat {BEA} = \widehat {BCA}\] (hai góc nội tiếp cùng chắn  của \(\left( O \right)\)), hay \(\widehat {BEA} = \widehat {SCA}\).

                Xét \(\Delta AEB\) và \(\Delta ACS\) có

                Suy ra: \(\frac{{AE}}{{AC}} = \frac{{AB}}{{AS}}\) (tỉ số đồng dạng) hay \(AB.AC = AE.AS\) (điều phải chứng minh).

                c) Vì \(H\) là trực tâm của \(\Delta ABC \Rightarrow BH \bot AC\) tại \(V \Rightarrow \widehat {AVH} = 90^\circ .\)

                Xét \(\Delta AVH\) và \(\Delta ADC\) có

                Mà \[\widehat {BEA} = \widehat {ACB}\] và \[\widehat {AHV} = \widehat {BHE}\] (hai góc đối đỉnh), suy ra \[\widehat {BEA} = \widehat {BHE}\] hay \[\widehat {BEH} = \widehat {BHE}\], khi đó \(\Delta BHE\) cân tại \(B\), có \(BD\) là đường cao nên \(BD\) cũng đồng thời là đường trung tuyến của \(\Delta BHE \Rightarrow DH = DE = \frac{{HE}}{2}\).

                Xét \(\Delta ABS\) và \(\Delta AEC\) có

                Có tứ giác \(BDEK\) nội tiếp nên \(\widehat {EKD} = \widehat {EBD}\) (hai góc nội tiếp cùng chắn  hay \(\widehat {EKD} = \widehat {EBC}\,)\)

                Lại có \(\widehat {EBC} = \widehat {EAC}\), suy ra \(\widehat {EKD} = \widehat {BAS}\).

                Xét \(\Delta ABS\) và \(\Delta KED\) có:

                Xét \(\Delta BIS\) và \(\Delta EKH\) có: \(\left\{ \begin{array}{l}\frac{{BI}}{{BS}} = \frac{{EK}}{{EH}}\\\widehat {IBS} = \widehat {KEH}\end{array} \right. \Rightarrow \widehat {BIS} = \widehat {EKH}\) (hai góc tương ứng).

                Gọi \(U\) là giao điểm của \(KH\) và \(IS\).

                Ta có: \(\widehat {BIS} + \widehat {IKH} = \widehat {EKH} + \widehat {IKH} = \widehat {EKA} = 90^\circ \) hay \(\widehat {KIU} + \widehat {IKU} = 90^\circ \).

                Xét \(\Delta IKU\) có \(\widehat {KIU} + \widehat {IKU} + \widehat {IUK} = 180^\circ \) (định lý tổng ba góc trong một tam giác).

                \( \Rightarrow \widehat {IUK} = 180^\circ  - \left( {\widehat {KIU} + \widehat {IKU}} \right) = 180^\circ  - 90^\circ  = 90^\circ  \Rightarrow IS \bot KH\) (điểu phải chứng minh).