PHẦN II. (4,0 điểm) Câu hỏi trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu thí sinh chọn đúng hoặc sai.
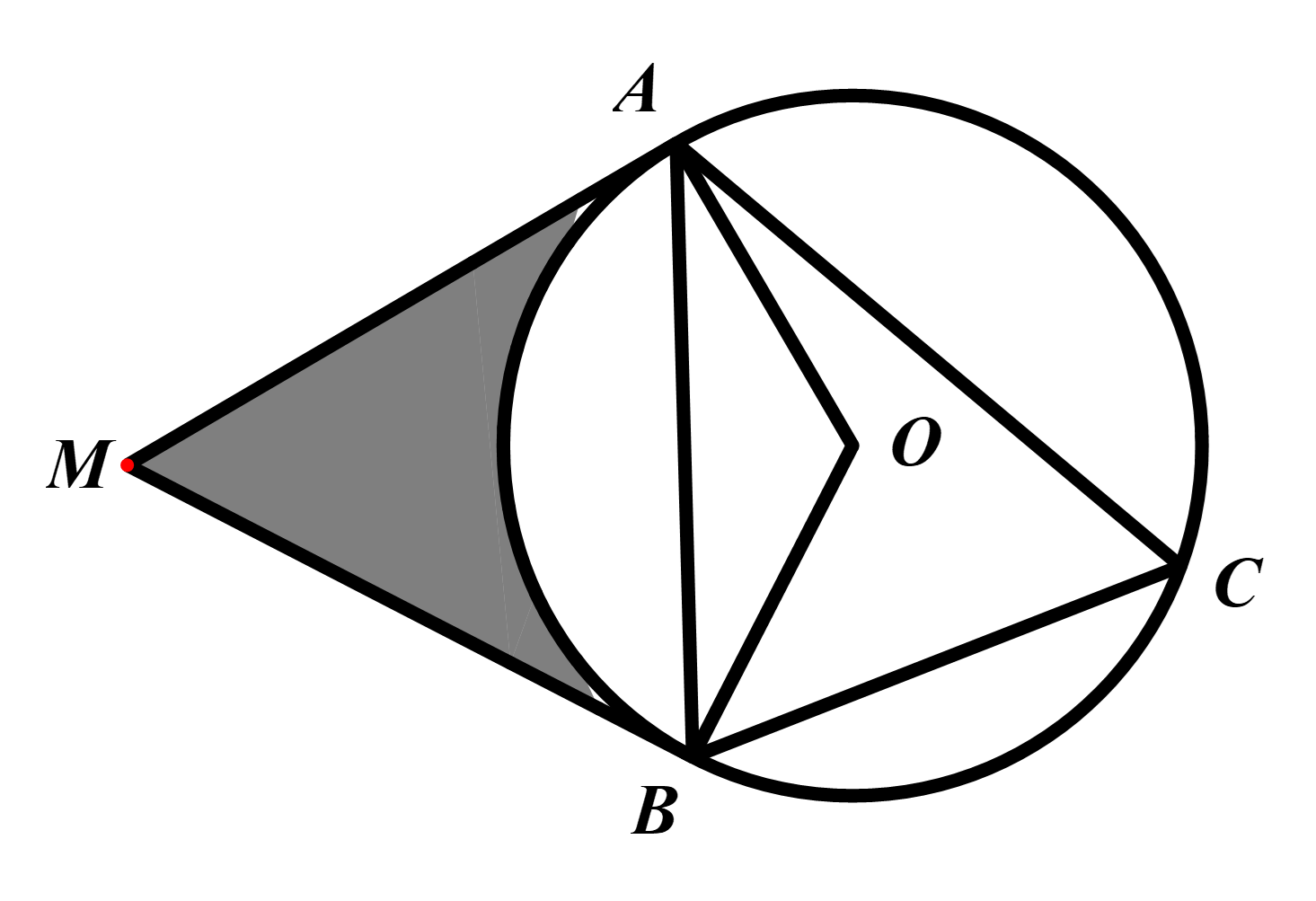
Cho \(\Delta ABC\) nhọn, nội tiếp đường tròn \(\left( {O;4cm} \right)\) và \(\widehat {ACB} = 60^\circ .\) Các tiếp tuyến tại \(A\) và \(B\) của đường tròn \(\left( {O;4cm} \right)\) cắt nhau tại \(M\).
PHẦN II. (4,0 điểm) Câu hỏi trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu thí sinh chọn đúng hoặc sai.

Quảng cáo
Trả lời:
a) Sai. \(\widehat {ACB} = 60^\circ \Rightarrow \widehat {AOB} = 120^\circ \Rightarrow \) sđ
b) Đúng. Vì xét \(\Delta OAM\) vuông tại \(A\) có \(\widehat {AMO} = 30^\circ \)
\( \Rightarrow AM = OA \cdot \cot 30^\circ = 4\sqrt 3 \left( {cm} \right)\)
c) Đúng. Vì \(\Delta AMO\) và \(\Delta BMO\) là các tam giác vuông
Chung cạnh huyền OM
d) Đúng
Vì \({S_{g/h}} = {S_{AMBO}} - {S_{qAOB}}\)
\( = 2.{S_{\Delta AMO}} - \frac{{\pi \cdot {4^2} \cdot 120}}{{360}} = 16\sqrt 3 - \frac{{16\pi }}{3} = 16\left( {\sqrt 3 - \frac{\pi }{3}} \right)\left( {c{m^2}} \right)\)
\( \Rightarrow S = {S_{AOBM}} - {S_q} = 16\sqrt 3 - \frac{{16\pi }}{3} = 16\left( {\frac{{3\sqrt 3 - \pi }}{3}} \right)\)
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
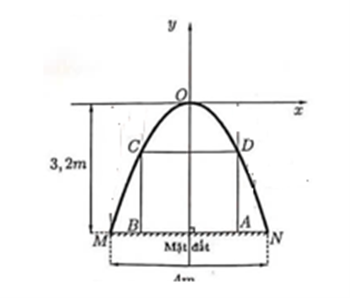
Gọi \[N({x_0},{y_0}),\]
Vì \[MN{\rm{ }} = {\rm{ }}4{\rm{ }} = > {x_0} = 2\]
Vì khoảng cách từ O đến MN là \[3,2 \Rightarrow {y_0} = - 3,2\]
Suy ra \[N\left( {2\,;\,\, - 3,2} \right)\]
Thay \[N\left( {2\,;\,\, - 3,2} \right)\] vào \[y = a{x^2}\] ta được
\[ - 3,2 = a \cdot {2^2}\]
\[a = - 3,2:4 = - 0,8\]
\[\;y = - 0,8{x^2}\]
Gọi \[AB = CD = 2u\] và \[D\left( {{x_1};{\rm{ }}{y_1}} \right)\] thuộc đường cong, suy ra \[{x_1} = {\rm{ }}u\]
mà \[{y_1} = - {\rm{ }}0.8{u^2}\]
\[ \Rightarrow {\rm{ }}D\left( {u; - 0,8{u^2}} \right)\]
\[ \Rightarrow {\rm{ }}AD{\rm{ }} = 3,2 - 0.8{u^2}\]
Chu vi hình ABCD là:
\[\begin{array}{l}P = (AB + AD) \cdot 2 = (2u + 3,2 - 0,8{u^2}) \cdot 2\\ = - 1,6{u^2} + 4u + 6,4\\ = - 1,6\left( {{u^2} - 2.5u + \frac{{25}}{{16}}} \right) + 8,9\\ = - 1,6{\left( {u - \frac{5}{4}} \right)^2} + 8,9 \le 8,9\end{array}\]
Lời giải
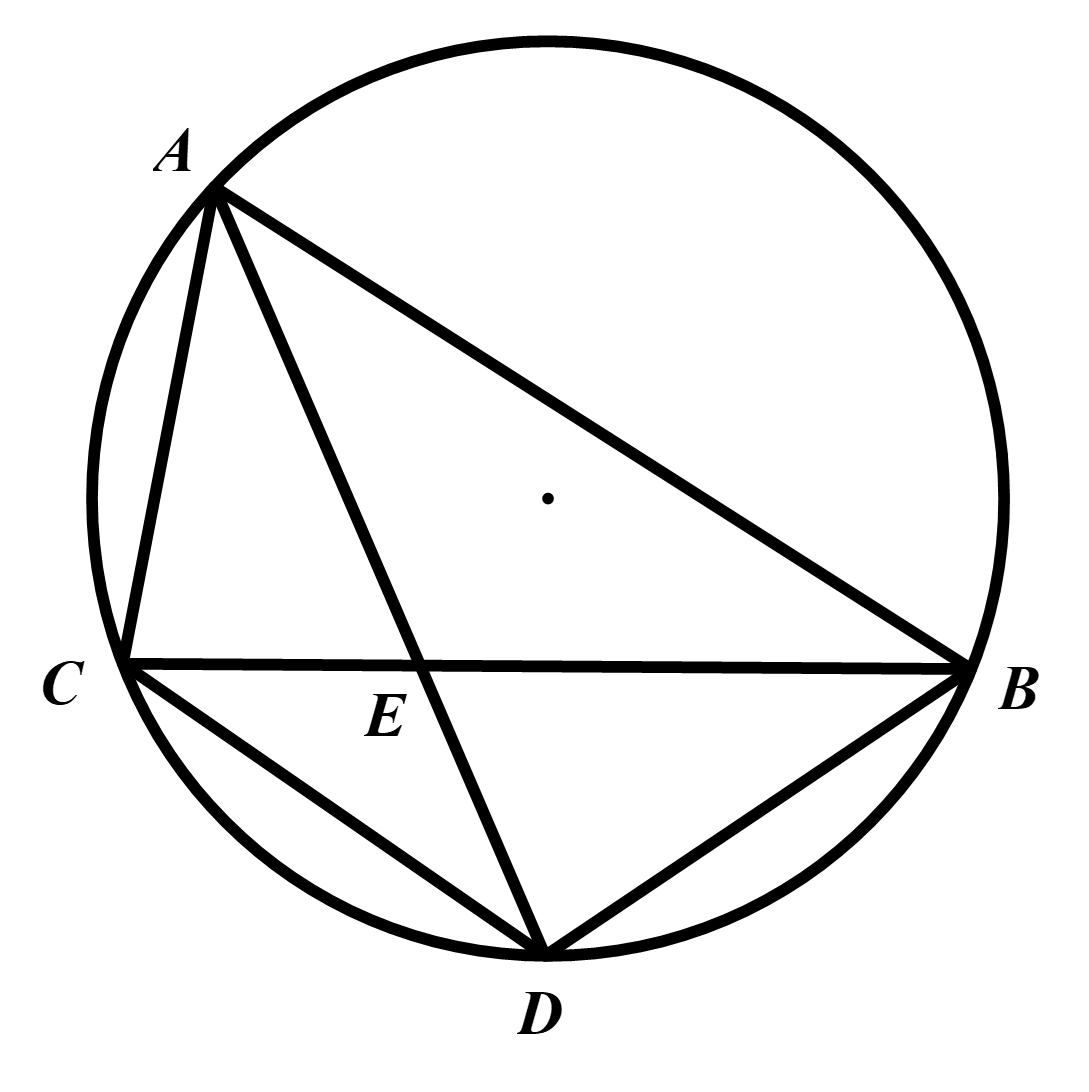
Lấy \((2) - (1) \Rightarrow AE(AD - ED) = AB \cdot AC - EB \cdot EC\)
\( \Rightarrow A{E^2} = AB \cdot AC - EB \cdot EC\quad (3)\)
Áp dụng tính chất phân giác \(\Delta ABC \Rightarrow \frac{{AC}}{{AB}} = \frac{{CE}}{{EB}} \Rightarrow \frac{{AC}}{{AC + AB}} = \frac{{CE}}{{CE + EB}}\)
thay số: \( \Rightarrow CE = \frac{{33,6 \cdot 61,6}}{{89,6}} = 23,1\)
Suy ra \(EB = 61,6 - 23,1 = 38,5\)
Thay vào (3) ta được \(A{E^2} = 33,6 \cdot 56 - 23,1 \cdot 38,5 = 992,25\)
\( \Rightarrow AE = 31,5\,\,km\)
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.