Tại vùng biển \(X\), có hai cảng biển ở vị trí các điểm \(A\) và \(B\), hai hòn đảo ở vị trí các điểm \(C\) và \(D\)Trong một cuộc thi tuyển dụng việc làm, ban tổ chức quy định mỗi người ứng tuyển phải trả lời 12 câu hỏi ở vòng sơ tuyển. Mỗi câu hỏi này có sẵn bốn phương án, trong đó chỉ có một phương án đúng. Người ứng tuyển chọn phương án đúng sẽ được cộng thêm 5 điểm, chọn phương án sai bị trừ đi 2 điểm. Ở vòng sơ tuyển, ban tổ chức tặng cho mỗi người dự thi 20 điểm và theo quy định người ứng tuyển phải trả lời hết 12 câu hỏi; người nào có số điểm từ 50 trở lên mới được dự thi vòng tiếp theo. Hỏi người ứng tuyển phải trả lời chính xác ít nhất bao nhiêu câu hỏi ở vòng sơ tuyển thì mới được vào vòng tiếp theo?
Tại vùng biển \(X\), có hai cảng biển ở vị trí các điểm \(A\) và \(B\), hai hòn đảo ở vị trí các điểm \(C\) và \(D\)Trong một cuộc thi tuyển dụng việc làm, ban tổ chức quy định mỗi người ứng tuyển phải trả lời 12 câu hỏi ở vòng sơ tuyển. Mỗi câu hỏi này có sẵn bốn phương án, trong đó chỉ có một phương án đúng. Người ứng tuyển chọn phương án đúng sẽ được cộng thêm 5 điểm, chọn phương án sai bị trừ đi 2 điểm. Ở vòng sơ tuyển, ban tổ chức tặng cho mỗi người dự thi 20 điểm và theo quy định người ứng tuyển phải trả lời hết 12 câu hỏi; người nào có số điểm từ 50 trở lên mới được dự thi vòng tiếp theo. Hỏi người ứng tuyển phải trả lời chính xác ít nhất bao nhiêu câu hỏi ở vòng sơ tuyển thì mới được vào vòng tiếp theo?
Quảng cáo
Trả lời:
Gọi số câu đúng là \(x\), \(x \in \mathbb{N}*,x < 12\), khi đó số câu sai là \(12 - x\).
Theo bài ra, ta có:
\(5x - 2\left( {12 - x} \right) + 20 \ge 50\)
\(7x \ge 54\)
\(x \ge \frac{{54}}{7} \approx 7,7\)
\(x \in \mathbb{N}*\), \({x_{min}} = 8\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
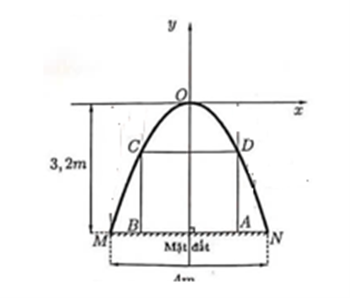
Gọi \[N({x_0},{y_0}),\]
Vì \[MN{\rm{ }} = {\rm{ }}4{\rm{ }} = > {x_0} = 2\]
Vì khoảng cách từ O đến MN là \[3,2 \Rightarrow {y_0} = - 3,2\]
Suy ra \[N\left( {2\,;\,\, - 3,2} \right)\]
Thay \[N\left( {2\,;\,\, - 3,2} \right)\] vào \[y = a{x^2}\] ta được
\[ - 3,2 = a \cdot {2^2}\]
\[a = - 3,2:4 = - 0,8\]
\[\;y = - 0,8{x^2}\]
Gọi \[AB = CD = 2u\] và \[D\left( {{x_1};{\rm{ }}{y_1}} \right)\] thuộc đường cong, suy ra \[{x_1} = {\rm{ }}u\]
mà \[{y_1} = - {\rm{ }}0.8{u^2}\]
\[ \Rightarrow {\rm{ }}D\left( {u; - 0,8{u^2}} \right)\]
\[ \Rightarrow {\rm{ }}AD{\rm{ }} = 3,2 - 0.8{u^2}\]
Chu vi hình ABCD là:
\[\begin{array}{l}P = (AB + AD) \cdot 2 = (2u + 3,2 - 0,8{u^2}) \cdot 2\\ = - 1,6{u^2} + 4u + 6,4\\ = - 1,6\left( {{u^2} - 2.5u + \frac{{25}}{{16}}} \right) + 8,9\\ = - 1,6{\left( {u - \frac{5}{4}} \right)^2} + 8,9 \le 8,9\end{array}\]
Lời giải
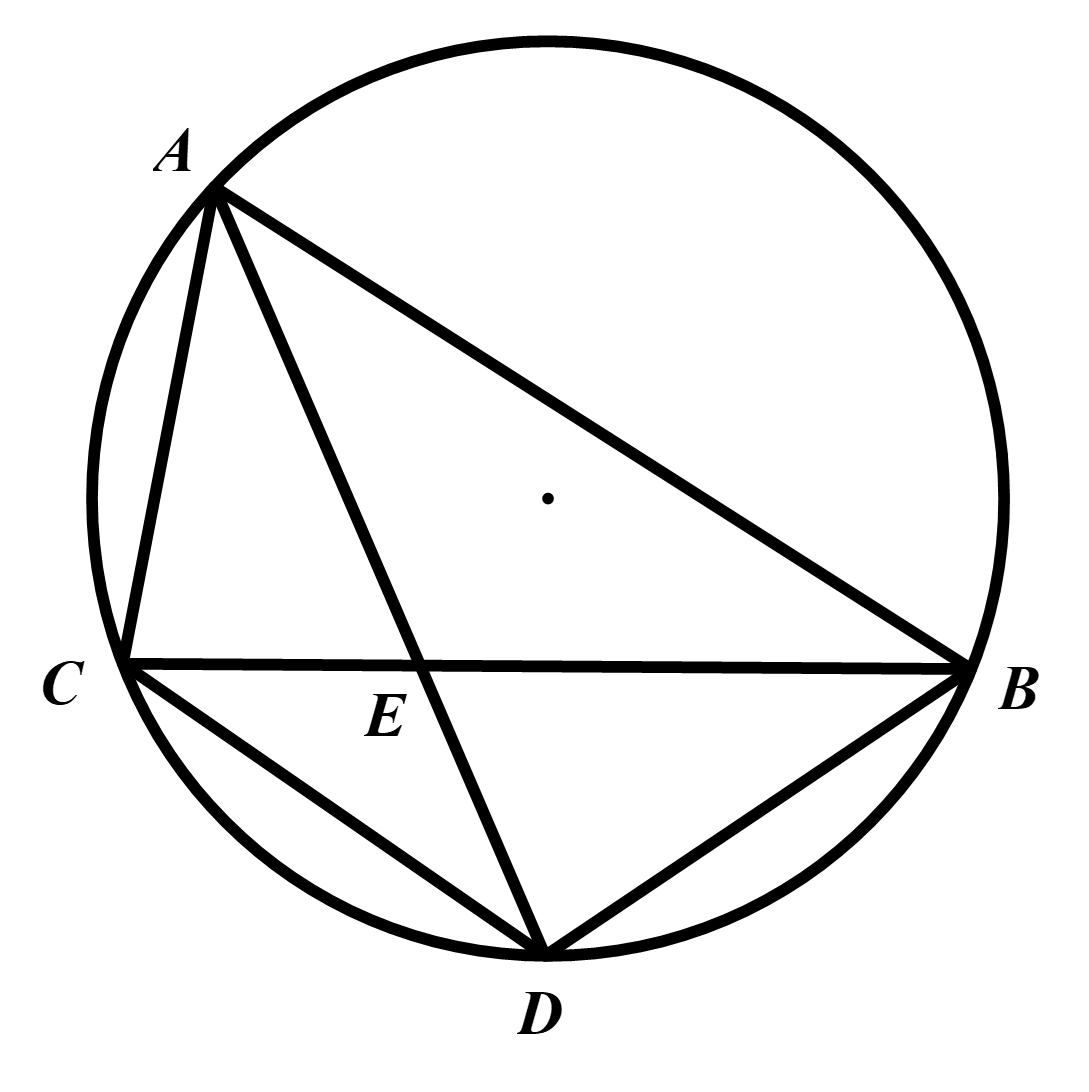
Lấy \((2) - (1) \Rightarrow AE(AD - ED) = AB \cdot AC - EB \cdot EC\)
\( \Rightarrow A{E^2} = AB \cdot AC - EB \cdot EC\quad (3)\)
Áp dụng tính chất phân giác \(\Delta ABC \Rightarrow \frac{{AC}}{{AB}} = \frac{{CE}}{{EB}} \Rightarrow \frac{{AC}}{{AC + AB}} = \frac{{CE}}{{CE + EB}}\)
thay số: \( \Rightarrow CE = \frac{{33,6 \cdot 61,6}}{{89,6}} = 23,1\)
Suy ra \(EB = 61,6 - 23,1 = 38,5\)
Thay vào (3) ta được \(A{E^2} = 33,6 \cdot 56 - 23,1 \cdot 38,5 = 992,25\)
\( \Rightarrow AE = 31,5\,\,km\)
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.