Tại vùng biển \(X\), có hai cảng biển ở vị trí các điểm \(A\) và \(B\), hai hòn đảo ở vị trí các điểm \(C\) và \(D\). Bốn điểm \(A,B,C,D\) cùng thuộc một đường tròn (được mô tả như hình vẽ). Biết rằng khoảng cách giữa các điểm như sau: \(AB = 56\) km, \(BC = 61,6\) km, \(AC = 33,6\) km và \(BD = CD\). Theo lịch trình vận chuyển, tàu từ cảng \(A\) cung cấp hàng cho đảo \(D\) ; tàu từ cảng \(B\) cung cấp hàng cho đảo \(C\). Nhưng trên thực tế, lượng hàng từ cảng \(A\) không đủ cung cấp cho đảo \(D\) nên phải lấy hàng bổ sung. Vì vậy hai chủ tàu thống nhất thực hiện đúng lịch trình như kế hoạch ban đầu \(\left( {A \to D\,;\,\,B \to C} \right)\) và sẽ gặp nhau ở vị trí điểm \(E\) (\(E\) là giao điểm của \(AD\) và \(BC\)) để bổ sung hàng hóa và tiết kiệm chi phí vận chuyển. Khoảng cách từ vị trí điểm \(A\) đến vị trí điểm \(E\) bằng bao nhiêu kilômét?
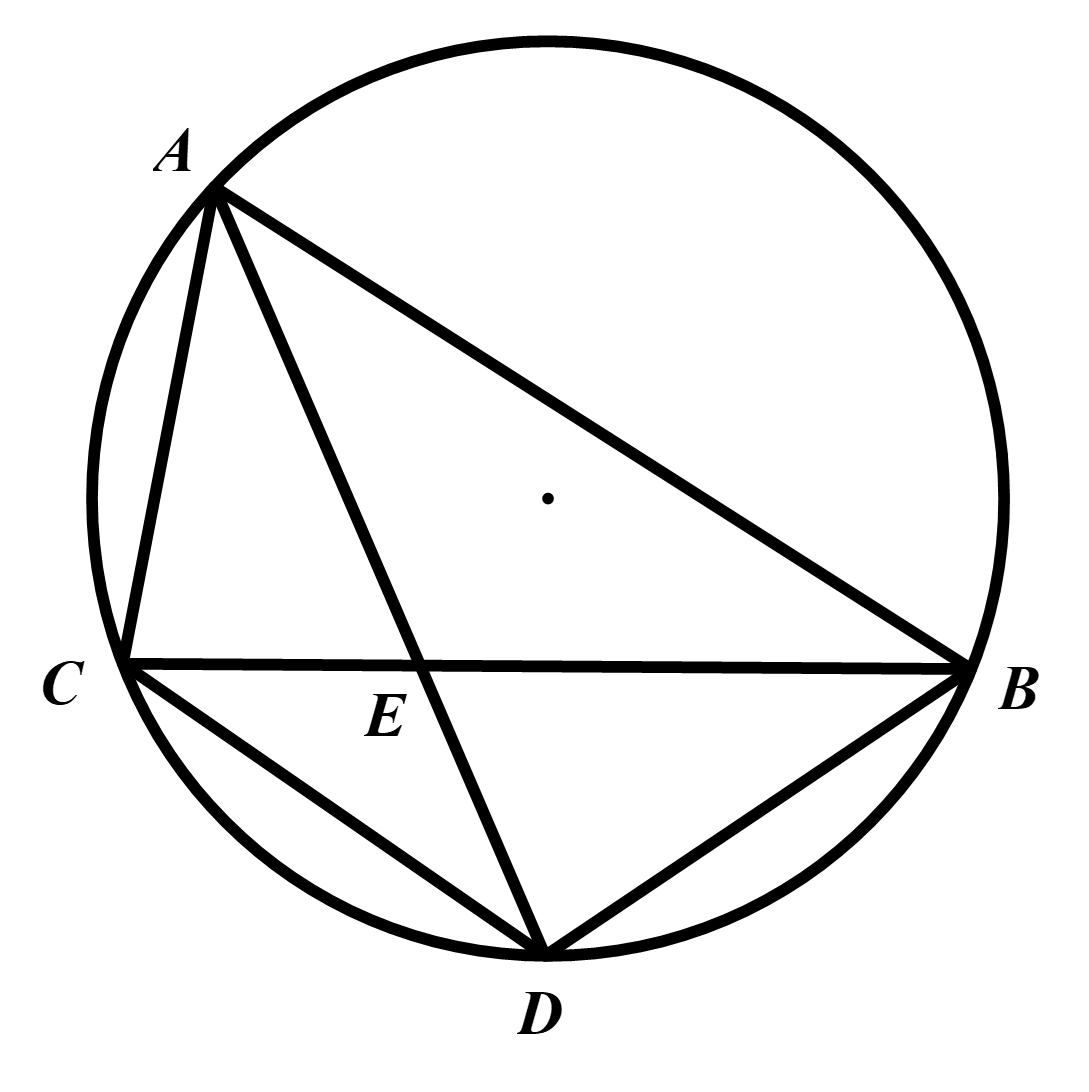
Tại vùng biển \(X\), có hai cảng biển ở vị trí các điểm \(A\) và \(B\), hai hòn đảo ở vị trí các điểm \(C\) và \(D\). Bốn điểm \(A,B,C,D\) cùng thuộc một đường tròn (được mô tả như hình vẽ). Biết rằng khoảng cách giữa các điểm như sau: \(AB = 56\) km, \(BC = 61,6\) km, \(AC = 33,6\) km và \(BD = CD\). Theo lịch trình vận chuyển, tàu từ cảng \(A\) cung cấp hàng cho đảo \(D\) ; tàu từ cảng \(B\) cung cấp hàng cho đảo \(C\). Nhưng trên thực tế, lượng hàng từ cảng \(A\) không đủ cung cấp cho đảo \(D\) nên phải lấy hàng bổ sung. Vì vậy hai chủ tàu thống nhất thực hiện đúng lịch trình như kế hoạch ban đầu \(\left( {A \to D\,;\,\,B \to C} \right)\) và sẽ gặp nhau ở vị trí điểm \(E\) (\(E\) là giao điểm của \(AD\) và \(BC\)) để bổ sung hàng hóa và tiết kiệm chi phí vận chuyển. Khoảng cách từ vị trí điểm \(A\) đến vị trí điểm \(E\) bằng bao nhiêu kilômét?

Quảng cáo
Trả lời:
Lấy \((2) - (1) \Rightarrow AE(AD - ED) = AB \cdot AC - EB \cdot EC\)
\( \Rightarrow A{E^2} = AB \cdot AC - EB \cdot EC\quad (3)\)
Áp dụng tính chất phân giác \(\Delta ABC \Rightarrow \frac{{AC}}{{AB}} = \frac{{CE}}{{EB}} \Rightarrow \frac{{AC}}{{AC + AB}} = \frac{{CE}}{{CE + EB}}\)
thay số: \( \Rightarrow CE = \frac{{33,6 \cdot 61,6}}{{89,6}} = 23,1\)
Suy ra \(EB = 61,6 - 23,1 = 38,5\)
Thay vào (3) ta được \(A{E^2} = 33,6 \cdot 56 - 23,1 \cdot 38,5 = 992,25\)
\( \Rightarrow AE = 31,5\,\,km\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
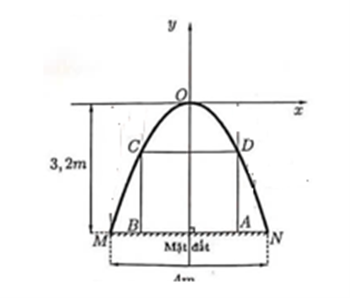
Gọi \[N({x_0},{y_0}),\]
Vì \[MN{\rm{ }} = {\rm{ }}4{\rm{ }} = > {x_0} = 2\]
Vì khoảng cách từ O đến MN là \[3,2 \Rightarrow {y_0} = - 3,2\]
Suy ra \[N\left( {2\,;\,\, - 3,2} \right)\]
Thay \[N\left( {2\,;\,\, - 3,2} \right)\] vào \[y = a{x^2}\] ta được
\[ - 3,2 = a \cdot {2^2}\]
\[a = - 3,2:4 = - 0,8\]
\[\;y = - 0,8{x^2}\]
Gọi \[AB = CD = 2u\] và \[D\left( {{x_1};{\rm{ }}{y_1}} \right)\] thuộc đường cong, suy ra \[{x_1} = {\rm{ }}u\]
mà \[{y_1} = - {\rm{ }}0.8{u^2}\]
\[ \Rightarrow {\rm{ }}D\left( {u; - 0,8{u^2}} \right)\]
\[ \Rightarrow {\rm{ }}AD{\rm{ }} = 3,2 - 0.8{u^2}\]
Chu vi hình ABCD là:
\[\begin{array}{l}P = (AB + AD) \cdot 2 = (2u + 3,2 - 0,8{u^2}) \cdot 2\\ = - 1,6{u^2} + 4u + 6,4\\ = - 1,6\left( {{u^2} - 2.5u + \frac{{25}}{{16}}} \right) + 8,9\\ = - 1,6{\left( {u - \frac{5}{4}} \right)^2} + 8,9 \le 8,9\end{array}\]
Câu 2
Lời giải
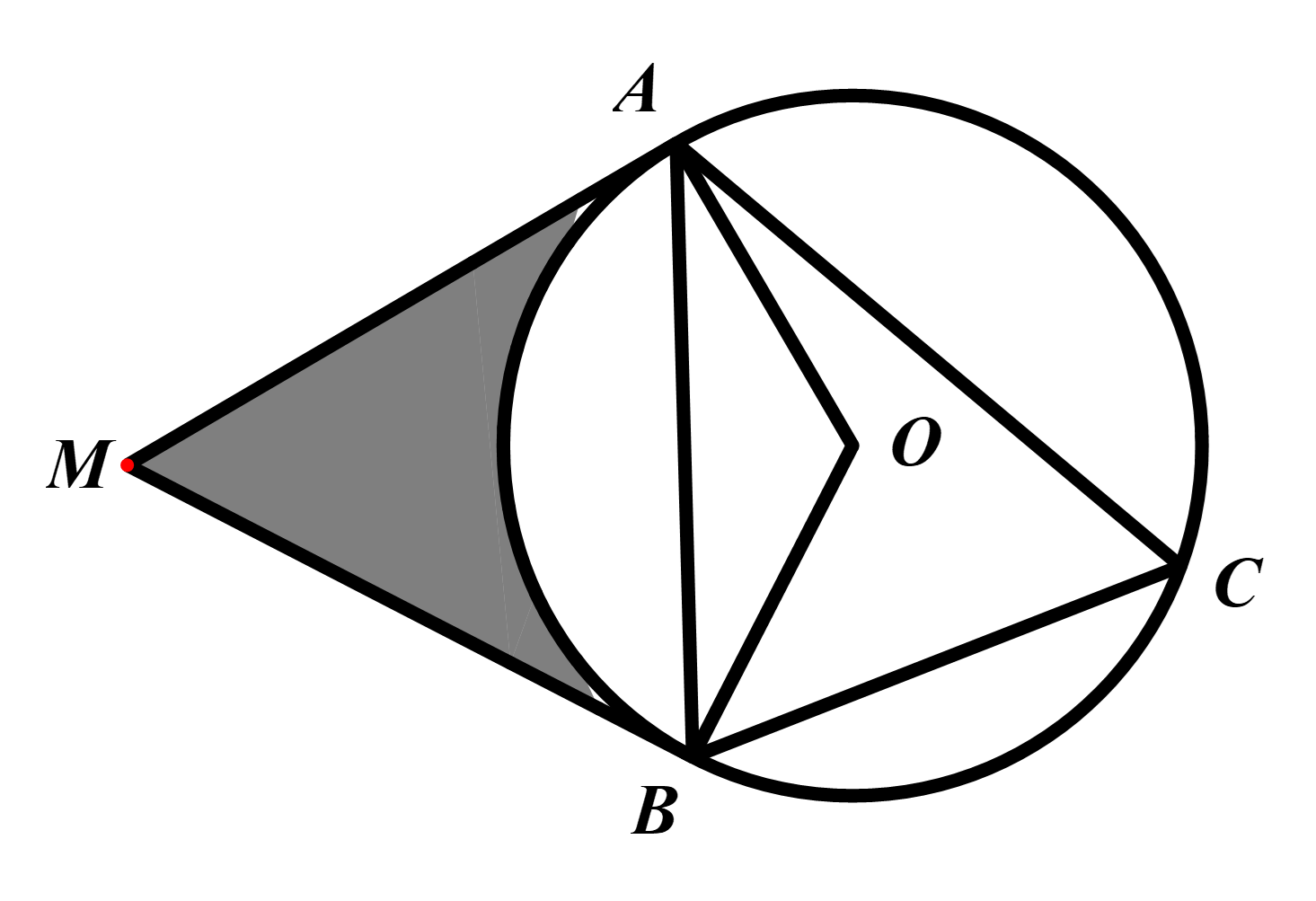
a) Sai. \(\widehat {ACB} = 60^\circ \Rightarrow \widehat {AOB} = 120^\circ \Rightarrow \) sđ
b) Đúng. Vì xét \(\Delta OAM\) vuông tại \(A\) có \(\widehat {AMO} = 30^\circ \)
\( \Rightarrow AM = OA \cdot \cot 30^\circ = 4\sqrt 3 \left( {cm} \right)\)
c) Đúng. Vì \(\Delta AMO\) và \(\Delta BMO\) là các tam giác vuông
Chung cạnh huyền OM
d) Đúng
Vì \({S_{g/h}} = {S_{AMBO}} - {S_{qAOB}}\)
\( = 2.{S_{\Delta AMO}} - \frac{{\pi \cdot {4^2} \cdot 120}}{{360}} = 16\sqrt 3 - \frac{{16\pi }}{3} = 16\left( {\sqrt 3 - \frac{\pi }{3}} \right)\left( {c{m^2}} \right)\)
\( \Rightarrow S = {S_{AOBM}} - {S_q} = 16\sqrt 3 - \frac{{16\pi }}{3} = 16\left( {\frac{{3\sqrt 3 - \pi }}{3}} \right)\)
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.