Cho hai biểu thức \(A = \left( {\sqrt {12} - \sqrt {27} + \sqrt {75} } \right):\sqrt 3 \) và \(B = \frac{{x + 4 + 4\sqrt x }}{{\sqrt x + 2}} + \frac{{x - \sqrt x }}{{\sqrt x - 1}}\).
a) Rút gọn biểu thức \(B\) ta được \(B = 2\sqrt x - 1\).
Đúng
Sai
b) Điều kiện xác định của biểu thức \(B\) là \(x \ge 0\) và \(x \ne 1\).
Đúng
Sai
c) Giá trị của biểu thức \(A\) bằng 4.
Đúng
Sai
d) Tổng các giá trị nguyên của \(x\) thỏa mãn hệ thức \(B - 2 \le A\) bằng 10.
Đúng
Sai
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Sai vì \(\frac{{\sqrt x (\sqrt x - 1)}}{{\sqrt x - 1}} + \frac{{{{(\sqrt x + 2)}^2}}}{{\sqrt x + 2}} = \sqrt x + 2 + \sqrt x + 2 = 2\sqrt x + 2\)
b) Đúng vì \(\left\{ {\begin{array}{*{20}{l}}{x \ge 0}\\{\sqrt x - 1 \ne 0}\end{array}} \right.\) nên \(\left\{ {\begin{array}{*{20}{l}}{x \ge 0}\\{x \ne 1}\end{array}} \right.\)
c) Đúng vì \(A = 4\sqrt 3 :\sqrt 3 = 4\)
d) Sai vì \(B - 2 \le A \to 2\sqrt x + 2 - 2 \le A \to 2\sqrt x \le 4 \to 2\sqrt x \le 2 \to \sqrt x \le 1 \to x \le 1\)
Mà \(x \ge 0,x \ne 1,x \in \mathbb{Z} \Rightarrow x \in \left\{ {0\,;\,\,2\,;\,\,3\,;\,\,4} \right\}.\)
Do đó, tập các giá trị là \(0 + 2 + 3 + 4 = 9\)
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
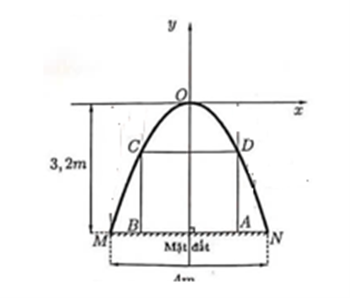
Gọi \[N({x_0},{y_0}),\]
Vì \[MN{\rm{ }} = {\rm{ }}4{\rm{ }} = > {x_0} = 2\]
Vì khoảng cách từ O đến MN là \[3,2 \Rightarrow {y_0} = - 3,2\]
Suy ra \[N\left( {2\,;\,\, - 3,2} \right)\]
Thay \[N\left( {2\,;\,\, - 3,2} \right)\] vào \[y = a{x^2}\] ta được
\[ - 3,2 = a \cdot {2^2}\]
\[a = - 3,2:4 = - 0,8\]
\[\;y = - 0,8{x^2}\]
Gọi \[AB = CD = 2u\] và \[D\left( {{x_1};{\rm{ }}{y_1}} \right)\] thuộc đường cong, suy ra \[{x_1} = {\rm{ }}u\]
mà \[{y_1} = - {\rm{ }}0.8{u^2}\]
\[ \Rightarrow {\rm{ }}D\left( {u; - 0,8{u^2}} \right)\]
\[ \Rightarrow {\rm{ }}AD{\rm{ }} = 3,2 - 0.8{u^2}\]
Chu vi hình ABCD là:
\[\begin{array}{l}P = (AB + AD) \cdot 2 = (2u + 3,2 - 0,8{u^2}) \cdot 2\\ = - 1,6{u^2} + 4u + 6,4\\ = - 1,6\left( {{u^2} - 2.5u + \frac{{25}}{{16}}} \right) + 8,9\\ = - 1,6{\left( {u - \frac{5}{4}} \right)^2} + 8,9 \le 8,9\end{array}\]
Lời giải
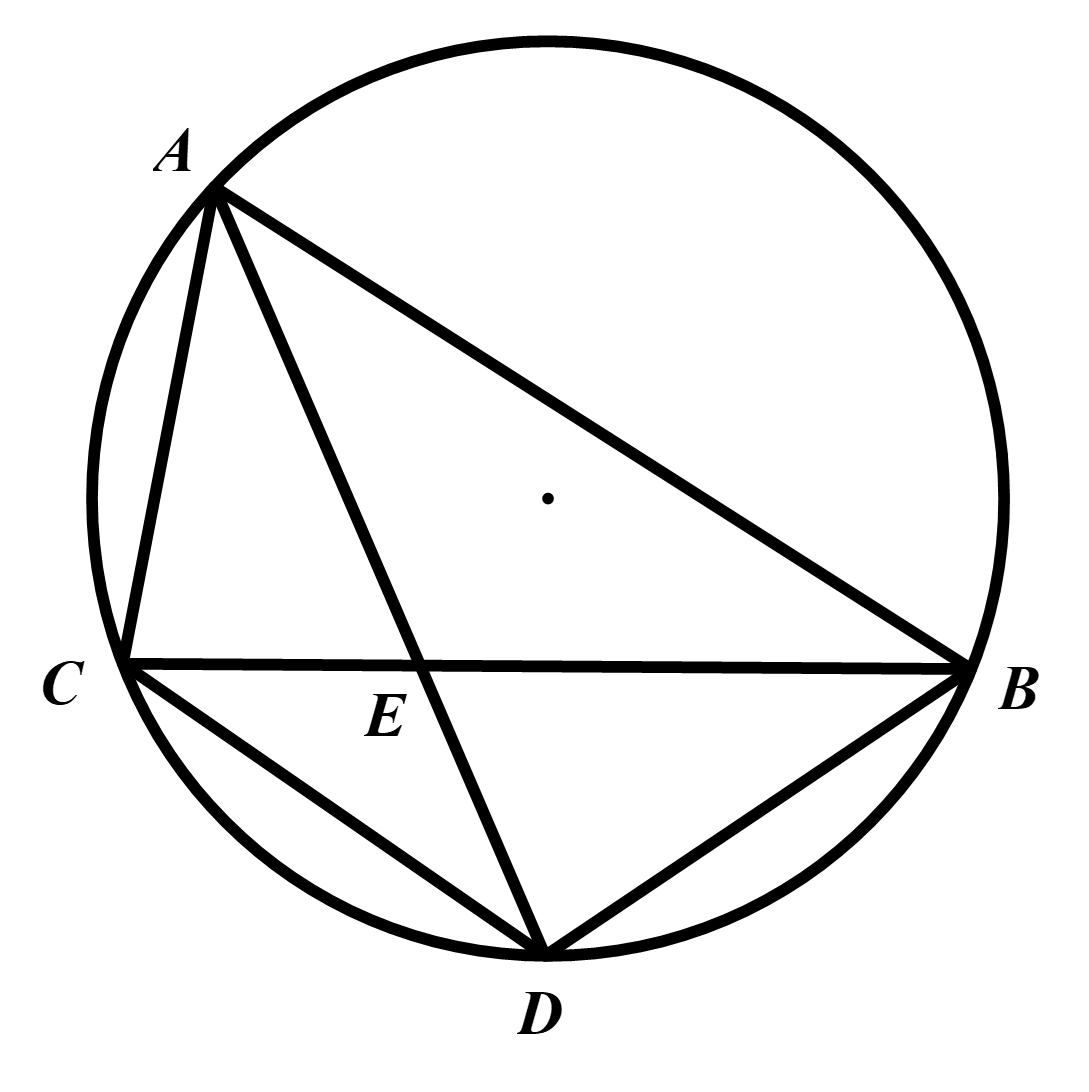
Lấy \((2) - (1) \Rightarrow AE(AD - ED) = AB \cdot AC - EB \cdot EC\)
\( \Rightarrow A{E^2} = AB \cdot AC - EB \cdot EC\quad (3)\)
Áp dụng tính chất phân giác \(\Delta ABC \Rightarrow \frac{{AC}}{{AB}} = \frac{{CE}}{{EB}} \Rightarrow \frac{{AC}}{{AC + AB}} = \frac{{CE}}{{CE + EB}}\)
thay số: \( \Rightarrow CE = \frac{{33,6 \cdot 61,6}}{{89,6}} = 23,1\)
Suy ra \(EB = 61,6 - 23,1 = 38,5\)
Thay vào (3) ta được \(A{E^2} = 33,6 \cdot 56 - 23,1 \cdot 38,5 = 992,25\)
\( \Rightarrow AE = 31,5\,\,km\)
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập