Phần III. (3,0 điểm) Câu hỏi trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6.
Cho hình nón có chiều cao \(h = 39\) cm và thể tích \(V = 1300\pi \) cm \(c{m^3}\). Độ dài đường sinh của hình nón đã cho bằng bao nhiêu centimét (làm tròn kết quả đến hàng phần mười)?
Phần III. (3,0 điểm) Câu hỏi trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6.
Cho hình nón có chiều cao \(h = 39\) cm và thể tích \(V = 1300\pi \) cm \(c{m^3}\). Độ dài đường sinh của hình nón đã cho bằng bao nhiêu centimét (làm tròn kết quả đến hàng phần mười)?
Quảng cáo
Trả lời:
Đáp án:
Điền đáp án: 40,3
Giải thích
\(\begin{array}{l}V = \frac{1}{3}\pi {R^2}h\\1300\pi = \frac{1}{3}\pi {R^2} \cdot 39\\{R^2} = 100\end{array}\)
Ta có: \(l = \sqrt {{R^2} + {h^2}} = \sqrt {100 + {{39}^2}} = \sqrt {1621} \approx 40,3(\;{\rm{cm}})\).
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
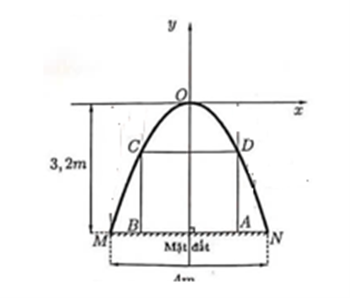
Gọi \[N({x_0},{y_0}),\]
Vì \[MN{\rm{ }} = {\rm{ }}4{\rm{ }} = > {x_0} = 2\]
Vì khoảng cách từ O đến MN là \[3,2 \Rightarrow {y_0} = - 3,2\]
Suy ra \[N\left( {2\,;\,\, - 3,2} \right)\]
Thay \[N\left( {2\,;\,\, - 3,2} \right)\] vào \[y = a{x^2}\] ta được
\[ - 3,2 = a \cdot {2^2}\]
\[a = - 3,2:4 = - 0,8\]
\[\;y = - 0,8{x^2}\]
Gọi \[AB = CD = 2u\] và \[D\left( {{x_1};{\rm{ }}{y_1}} \right)\] thuộc đường cong, suy ra \[{x_1} = {\rm{ }}u\]
mà \[{y_1} = - {\rm{ }}0.8{u^2}\]
\[ \Rightarrow {\rm{ }}D\left( {u; - 0,8{u^2}} \right)\]
\[ \Rightarrow {\rm{ }}AD{\rm{ }} = 3,2 - 0.8{u^2}\]
Chu vi hình ABCD là:
\[\begin{array}{l}P = (AB + AD) \cdot 2 = (2u + 3,2 - 0,8{u^2}) \cdot 2\\ = - 1,6{u^2} + 4u + 6,4\\ = - 1,6\left( {{u^2} - 2.5u + \frac{{25}}{{16}}} \right) + 8,9\\ = - 1,6{\left( {u - \frac{5}{4}} \right)^2} + 8,9 \le 8,9\end{array}\]
Lời giải
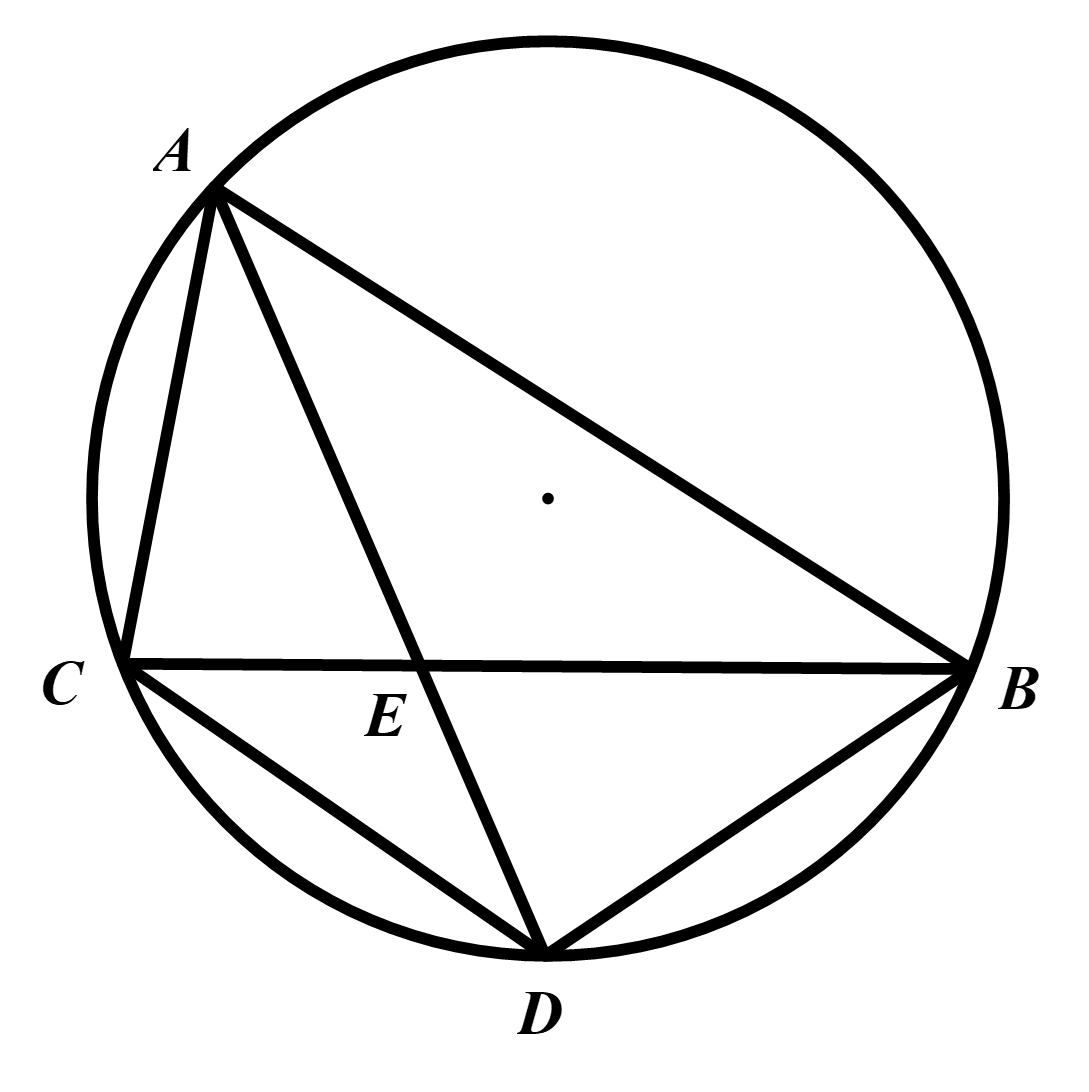
Lấy \((2) - (1) \Rightarrow AE(AD - ED) = AB \cdot AC - EB \cdot EC\)
\( \Rightarrow A{E^2} = AB \cdot AC - EB \cdot EC\quad (3)\)
Áp dụng tính chất phân giác \(\Delta ABC \Rightarrow \frac{{AC}}{{AB}} = \frac{{CE}}{{EB}} \Rightarrow \frac{{AC}}{{AC + AB}} = \frac{{CE}}{{CE + EB}}\)
thay số: \( \Rightarrow CE = \frac{{33,6 \cdot 61,6}}{{89,6}} = 23,1\)
Suy ra \(EB = 61,6 - 23,1 = 38,5\)
Thay vào (3) ta được \(A{E^2} = 33,6 \cdot 56 - 23,1 \cdot 38,5 = 992,25\)
\( \Rightarrow AE = 31,5\,\,km\)
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.