Một cửa hầm lò khai thác khoáng sản có dạng parabol \(y = a{x^2}\) (\(a \ne 0\)) trong mặt phẳng tọa độ \(Oxy\). Biết rằng \(Ox\) song song với đường thẳng \(MN\) (\(M,N\) là hai chân của cửa hầm lò và nằm trên mặt đất; giả sử mặt đất bằng phẳng) và \(x,y\) được tính theo đơn vị mét. Khoảng cách giữa hai chân cửa hầm lò \(MN = 4\) m; khoảng cách từ điểm \(O\) đến đường thẳng \(MN\) bằng 3,2 m. Người ta thường gia cố cho cửa hầm lò bằng một khung thép hình chữ nhật \(ABCD\) sao cho hai đỉnh \(A\) và \(B\) của khung thép chạm đất, hai đỉnh \(C\) và \(D\) của khung thép chạm vào cửa hầm lò (được mô tả như hình vẽ). Giá trị lớn nhất của chu vi hình chữ nhật \(ABCD\) tạo bởi khung thép trên bằng bao nhiêu mét?
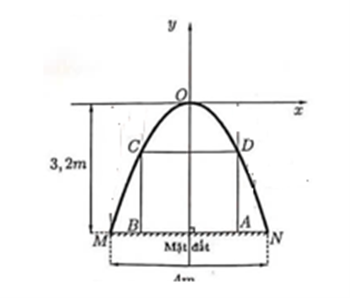
Một cửa hầm lò khai thác khoáng sản có dạng parabol \(y = a{x^2}\) (\(a \ne 0\)) trong mặt phẳng tọa độ \(Oxy\). Biết rằng \(Ox\) song song với đường thẳng \(MN\) (\(M,N\) là hai chân của cửa hầm lò và nằm trên mặt đất; giả sử mặt đất bằng phẳng) và \(x,y\) được tính theo đơn vị mét. Khoảng cách giữa hai chân cửa hầm lò \(MN = 4\) m; khoảng cách từ điểm \(O\) đến đường thẳng \(MN\) bằng 3,2 m. Người ta thường gia cố cho cửa hầm lò bằng một khung thép hình chữ nhật \(ABCD\) sao cho hai đỉnh \(A\) và \(B\) của khung thép chạm đất, hai đỉnh \(C\) và \(D\) của khung thép chạm vào cửa hầm lò (được mô tả như hình vẽ). Giá trị lớn nhất của chu vi hình chữ nhật \(ABCD\) tạo bởi khung thép trên bằng bao nhiêu mét?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi \[N({x_0},{y_0}),\]
Vì \[MN{\rm{ }} = {\rm{ }}4{\rm{ }} = > {x_0} = 2\]
Vì khoảng cách từ O đến MN là \[3,2 \Rightarrow {y_0} = - 3,2\]
Suy ra \[N\left( {2\,;\,\, - 3,2} \right)\]
Thay \[N\left( {2\,;\,\, - 3,2} \right)\] vào \[y = a{x^2}\] ta được
\[ - 3,2 = a \cdot {2^2}\]
\[a = - 3,2:4 = - 0,8\]
\[\;y = - 0,8{x^2}\]
Gọi \[AB = CD = 2u\] và \[D\left( {{x_1};{\rm{ }}{y_1}} \right)\] thuộc đường cong, suy ra \[{x_1} = {\rm{ }}u\]
mà \[{y_1} = - {\rm{ }}0.8{u^2}\]
\[ \Rightarrow {\rm{ }}D\left( {u; - 0,8{u^2}} \right)\]
\[ \Rightarrow {\rm{ }}AD{\rm{ }} = 3,2 - 0.8{u^2}\]
Chu vi hình ABCD là:
\[\begin{array}{l}P = (AB + AD) \cdot 2 = (2u + 3,2 - 0,8{u^2}) \cdot 2\\ = - 1,6{u^2} + 4u + 6,4\\ = - 1,6\left( {{u^2} - 2.5u + \frac{{25}}{{16}}} \right) + 8,9\\ = - 1,6{\left( {u - \frac{5}{4}} \right)^2} + 8,9 \le 8,9\end{array}\]
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lấy \((2) - (1) \Rightarrow AE(AD - ED) = AB \cdot AC - EB \cdot EC\)
\( \Rightarrow A{E^2} = AB \cdot AC - EB \cdot EC\quad (3)\)
Áp dụng tính chất phân giác \(\Delta ABC \Rightarrow \frac{{AC}}{{AB}} = \frac{{CE}}{{EB}} \Rightarrow \frac{{AC}}{{AC + AB}} = \frac{{CE}}{{CE + EB}}\)
thay số: \( \Rightarrow CE = \frac{{33,6 \cdot 61,6}}{{89,6}} = 23,1\)
Suy ra \(EB = 61,6 - 23,1 = 38,5\)
Thay vào (3) ta được \(A{E^2} = 33,6 \cdot 56 - 23,1 \cdot 38,5 = 992,25\)
\( \Rightarrow AE = 31,5\,\,km\)
Câu 2
a) Rút gọn biểu thức \(B\) ta được \(B = 2\sqrt x - 1\).
Đúng
Sai
b) Điều kiện xác định của biểu thức \(B\) là \(x \ge 0\) và \(x \ne 1\).
Đúng
Sai
c) Giá trị của biểu thức \(A\) bằng 4.
Đúng
Sai
d) Tổng các giá trị nguyên của \(x\) thỏa mãn hệ thức \(B - 2 \le A\) bằng 10.
Đúng
Sai
Lời giải
a) Sai vì \(\frac{{\sqrt x (\sqrt x - 1)}}{{\sqrt x - 1}} + \frac{{{{(\sqrt x + 2)}^2}}}{{\sqrt x + 2}} = \sqrt x + 2 + \sqrt x + 2 = 2\sqrt x + 2\)
b) Đúng vì \(\left\{ {\begin{array}{*{20}{l}}{x \ge 0}\\{\sqrt x - 1 \ne 0}\end{array}} \right.\) nên \(\left\{ {\begin{array}{*{20}{l}}{x \ge 0}\\{x \ne 1}\end{array}} \right.\)
c) Đúng vì \(A = 4\sqrt 3 :\sqrt 3 = 4\)
d) Sai vì \(B - 2 \le A \to 2\sqrt x + 2 - 2 \le A \to 2\sqrt x \le 4 \to 2\sqrt x \le 2 \to \sqrt x \le 1 \to x \le 1\)
Mà \(x \ge 0,x \ne 1,x \in \mathbb{Z} \Rightarrow x \in \left\{ {0\,;\,\,2\,;\,\,3\,;\,\,4} \right\}.\)
Do đó, tập các giá trị là \(0 + 2 + 3 + 4 = 9\)
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập