Các ăng ten parabol thu sóng hoạt động dựa theo nguyên lý: mọi tia sóng song song với trục của parabol đều có tia phản xạ đi qua tiêu điểm \[F\] của parabol (vì vậy nếu ta đặt thiết bị thu sóng tại \[F\] thì sẽ thu sóng được tốt nhất). Người ta chứng minh được rằng: Nếu đường thẳng vuông góc với trục của parabol tại \[F\] cắt parabol tại 2 điểm \[A,B\]thì \[OF = \frac{1}{4}AB\] với \[O\] là đỉnh của parabol (tham khảo hình vẽ).
Tính độ dài đoạn \[OF\]ứng với mô hình trên của một ăng ten parabol (ngang 90cm và cao 9cm).
Các ăng ten parabol thu sóng hoạt động dựa theo nguyên lý: mọi tia sóng song song với trục của parabol đều có tia phản xạ đi qua tiêu điểm \[F\] của parabol (vì vậy nếu ta đặt thiết bị thu sóng tại \[F\] thì sẽ thu sóng được tốt nhất). Người ta chứng minh được rằng: Nếu đường thẳng vuông góc với trục của parabol tại \[F\] cắt parabol tại 2 điểm \[A,B\]thì \[OF = \frac{1}{4}AB\] với \[O\] là đỉnh của parabol (tham khảo hình vẽ).
Tính độ dài đoạn \[OF\]ứng với mô hình trên của một ăng ten parabol (ngang 90cm và cao 9cm).
Câu hỏi trong đề: 5 bài tập Toán thực tế (có lời giải) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
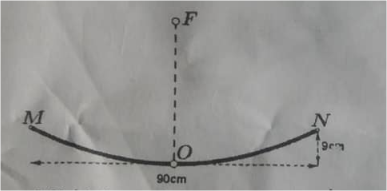
Ta có \[\left( P \right):y = a{x^2}\] đi qua điểm \[N\left( {45;9} \right)\]
Do đó \[9 = a{.45^2}\]
Nên \[a = \frac{1}{{225}}\]. Suy ra \[y = \frac{1}{{225}}{x^2}\]
Đường thẳng vuông góc \[Oy\] tại \[F\]cắt \[\left( P \right)\] tại \[A,B\] với \[{x_B} > 0\]
Vì \[{y_B} = OF = \frac{1}{4}AB = \frac{1}{2}FB = \frac{1}{2}{x_B}\] và \[B \in \left( P \right)\] nên \[\frac{1}{2}{x_B} = \frac{{x_B^2}}{{225}} \Leftrightarrow {x_B} = \frac{{225}}{2}\]
Vì vậy \[OF = \frac{1}{2}{x_B} = \frac{{225}}{4} = 56,25\left( {cm} \right)\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Giả sử trên mặt phẳng tọa độ, độ dài các đoạn thẳng được tính theo đơn vị mét.
Do khoảng cách giữa hai chân cổng là 4 m nên \(MA = NA = 2m\).
Theo giả thiết ta có \(OM = ON = 2\sqrt 5 \), áp dụng định lý Pythagore ta tính được: \(OA = 4\) vậy \(M\left( {2; - 4} \right),N\left( { - 2; - 4} \right)\).
Do \(M\left( {2; - 4} \right)\) thuộc parabol nên tọa độ điểm \(M\) thỏa mãn phương trình: \(\left( P \right):y = a{x^2}\) hay \( - 4 = a{.2^2} \Rightarrow a = - 1\) và \(\left( P \right):y = - {x^2}\).
b) Để đáp ứng chiều cao trước hết xe tải phải đi vào chính giữa cổng.
Xét đường thẳng \(\left( d \right):y = - \frac{3}{2}\)
(ứng với chiều cao của xe). Đường thẳng này cắt Parabol tại 2 điểm có tọa độ thỏa mãn hệ:
\(\left\{ \begin{array}{l}y = - {x^2}\\y = - \frac{3}{2}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x^2} = \frac{3}{2}\\y = - \frac{3}{2}\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x = \frac{{3\sqrt 2 }}{2};y = - \frac{3}{2}\\x = - \frac{{3\sqrt 2 }}{2};y = - \frac{3}{2}\end{array} \right.\)
suy ra tọa độ hai giao điểm là \(T\left( { - \frac{{3\sqrt 2 }}{2}; - \frac{3}{2}} \right);H\left( {\frac{{3\sqrt 2 }}{2};\frac{3}{2}} \right) \Rightarrow HT = 3\sqrt 2 > 2,4\).
Vậy xe tải có thể đi qua cổng.
Lời giải
a) Áp dụng công thức \({\rm{h}} = 9,8.{{\rm{t}}^2}\) ta có: \({\rm{t}} = 3\;{\rm{s}} \Rightarrow {\rm{h}} = 9,{8.3^2} = 88,2(\;{\rm{m}})\).
Vậy hang này sâu \(88,2\;{\rm{m}}\).
b) Áp dụng công thức \(h = 9,8.{{\rm{t}}^2}\) ta có: \({\rm{h}} = 156,8(\;{\rm{m}}) \Rightarrow {{\rm{t}}^2} = \frac{{156,8}}{{9,8}} = 16 \Rightarrow {\rm{t}} = 4\) (s)
Vậy mất 4 giây để hòn đá chạm đất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập