Rađa của một máy bay trực thăng theo dõi chuyển động của một ô tô trong \(10\) phút, phát hiện rằng vận tốc \(v\) của ô tô thay đổi phụ thuộc vào thời gian bởi công thức :
\(v = 3{t^2} - 30t + 135\)
(\(t\) tính bằng phút, \(v\) tính bằng km/h).
a) Tính vận tốc của ô tô khi \(t = 5\)phút.
b) Tính giá trị của \(t\) khi vận tốc ô tôt bằng \(120\) km/h (làm tròn kết quả đến chữ số thập phân thứ hai).
Rađa của một máy bay trực thăng theo dõi chuyển động của một ô tô trong \(10\) phút, phát hiện rằng vận tốc \(v\) của ô tô thay đổi phụ thuộc vào thời gian bởi công thức :
\(v = 3{t^2} - 30t + 135\)
(\(t\) tính bằng phút, \(v\) tính bằng km/h).
a) Tính vận tốc của ô tô khi \(t = 5\)phút.
b) Tính giá trị của \(t\) khi vận tốc ô tôt bằng \(120\) km/h (làm tròn kết quả đến chữ số thập phân thứ hai).
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Tính vận tốc của ô tô khi \(t = 5\)phút.
Khi \(t = 5\)(phút) thì \(v = {3.5^2} - 30.5 + 135 = 60\)(km/h)
b) Khi \(120\)(km/h) để tìm ra \(t\) ta giải phương trình:
\[\begin{array}{l}120 = 3{t^2} - 30t + 135\\3{t^2} - 30t + 15 = 0\end{array}\]
\[{t^2} - 10t + 5 = 0;\Delta ' = 25 - 5 = 20,\sqrt {\Delta '} = 2\sqrt 5 \]
\({t_1} = 5 + 2\sqrt 5 \approx 9,47;\,\,\,\,{t_2} = 5 - 2\sqrt 5 \approx 0,53\)
Vì rađa chỉ theo dõi trong \(10\)phút nên \(0 < t < 10\) do đó cả hai giá trị của \(t\) đều thích hợp.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
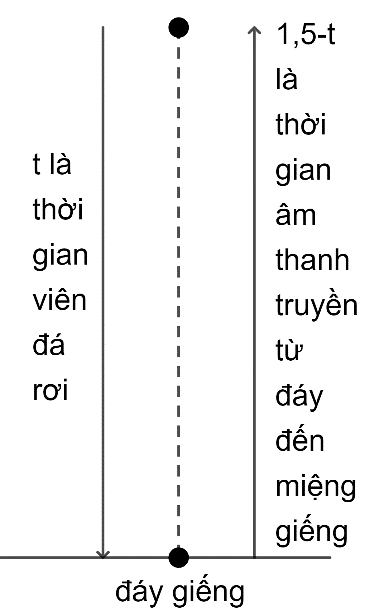
Gọi thời gian rơi của hòn đá từ miệng giếng đến đáy giếng là \[t\](\(0 < t < 1,5\) giây)
Suy ra thời gian âm thanh truyền từ đáy giếng đến miệng giếng là \(1,5 - t\) (giây)
Quãng đường mà hòn đá rơi được: \({S_1} = 5{t^2}\)
Quãng đường mà âm thanh truyền được: \({S_2} = 340.\left( {1,5 - t} \right)\)
Vì quãng đường mà hòn đá rơi được bằng quãng đường mà âm thanh truyền được (chính là khoảng cách từ miệng giếng đến đáy giếng), nên ta có phương trình:
\({S_1} = {S_2}\)\( \Rightarrow 5{t^2} = 340.\left( {1,5 - t} \right)\)\( \Rightarrow 5{t^2} = 510 - 340t\)\( \Rightarrow 5{t^2} + 340t - 510 = 0\)
\( \Rightarrow {t^2} + 68t - 102 = 0\,\,\left( {a = 1;\,\,b' = 34;\,\,c = 102} \right)\)
\({\rm{\Delta '}} = {\left( {b'} \right)^2} - ac = {34^2} - 1.\left( { - 102} \right) = 1258\); \(\sqrt {{\rm{\Delta '}}} = \sqrt {1258} \)
Phương trình có hai nghiệm:
\({x_1} = \frac{{ - b' + \sqrt {{\rm{\Delta '}}} }}{a} = \frac{{ - 34 + \sqrt {1258} }}{1} = 1,46\) (nhận);
\({x_2} = \frac{{ - b' - \sqrt {{\rm{\Delta '}}} }}{a} = \frac{{ - 34 - \sqrt {1258} }}{1} = - 69,46 < 0\)(loại)
Vậy: Thời gian rơi của hòn đá từ miệng giếng đến đáy giếng là \(t = 1,46\) giây. Độ sâu của cái giếng là: \(S = 5.1,{46^2} = 11\) mét.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập