Một mảnh đất hình chữ nhật có diện tích 240\({m^2}\). Nếu tăng chiều rộng lên 3m và giảm chiều dài 4m thì diện tích mảnh đất không đổi. Tính kích thước của mảnh đất?

Gọi chiều dài hình chữ nhật là \(x\,(\;{\rm{cm}},x > 0)\).

Chiều rộng hình chữ nhật là \(\frac{2}{3}x\,(\;{\rm{cm}})\).

Theo đầu bài, ta có phương trình:

\(x \cdot \frac{2}{3}x = 5400 \Leftrightarrow {x^2} = 8100 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 90}\\{x =  - 90{\rm{ (loai) }}}\end{array}} \right.\).

Vậy chiều dài hình chữ nhật là \(90\;{\rm{cm}}\), chiều rộng hình chữ nhật là \(60\;{\rm{cm}}\).

Do đó, chu vi hình chữ nhật là \((90 + 60) \cdot 2 = 300\;{\rm{cm}}\).

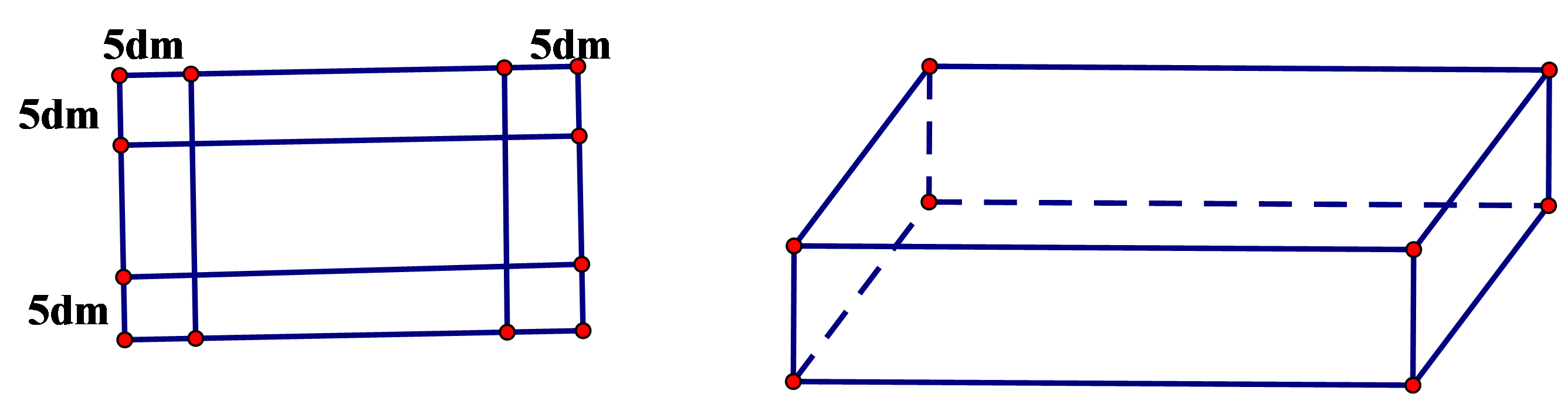
Gọi chiều rộng của miếng tôn lúc đầu là x (dm), \(x > 0\)

Chiều dài của nó là 2x (dm)

Khi làm thành một cái thùng không nắp thì chiều dài của thùng là \(2x - 10\) (dm), chiều rộng là \(x - 10\) (dm), chiều cao là 5dm.

Dung tích của thùng là \(5(2x - 10)(x - 10)(d{m^3})\)

Theo đầu bài ta có phương trình \(5(2x - 10)(x - 10) = 1500 \Leftrightarrow {x^2} - 15x - 100 = 0\)

Giải phương trình \(\Delta  = 225 + 400 = 625,\sqrt \Delta   = 25\)

Phương trình có nghiệm \({x_1} = 20,{x_2} =  - 5\) (loại)

Trả lời: Miếng tôn có chiều rộng bằng 20dm, chiều rộng bằng 40dm.