3 bài tập Toán Có Nội Dung Hình Học (có lời giải)

Gọi chiều rộng của mảnh đất là x (m), \(x > 0\)

Vì diện tích của mạnh đất bằng 240\({m^2}\)nên chiều dài là \(\frac{{240}}{x}\) (m)
Nếu tăng chiều rộng 3m và giảm chiều dài 4m thì mảnh đất mới có chiều rộng là \(x + 3\) (m), chiều dài là \(\left( {\frac{{240}}{x} - 4} \right)\) (m) và diện tích là \((x + 3)\left( {\frac{{240}}{x} - 4} \right)({m^2})\)

Theo đầu bài ta có phương trình \((x + 3)\left( {\frac{{240}}{x} - 4} \right) = 240\)

Vì \(x > 0\) nên từ phương trình này suy ra

\(\) \( - 4{x^2} - 12x + 240x + 720 = 240x \Leftrightarrow {x^2} + 3x - 180 = 0\)

Giải phương trình \(\Delta  = {3^2} + 720 = 729,\sqrt \Delta   = 27\)

Phương trình có nghiệm \({x_1} = 12,{x_2} =  - 15\) (loại)

Do đó, chiều rộng là 12m, chiều dài là  \(240:12 = 20\) (m)

Trả lời: Mảnh đất có chiều rộng là 12m, chiều dài là 20m.

Gọi chiều dài hình chữ nhật là \(x\,(\;{\rm{cm}},x > 0)\).

Chiều rộng hình chữ nhật là \(\frac{2}{3}x\,(\;{\rm{cm}})\).

Theo đầu bài, ta có phương trình:

\(x \cdot \frac{2}{3}x = 5400 \Leftrightarrow {x^2} = 8100 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 90}\\{x =  - 90{\rm{ (loai) }}}\end{array}} \right.\).

Vậy chiều dài hình chữ nhật là \(90\;{\rm{cm}}\), chiều rộng hình chữ nhật là \(60\;{\rm{cm}}\).

Do đó, chu vi hình chữ nhật là \((90 + 60) \cdot 2 = 300\;{\rm{cm}}\).

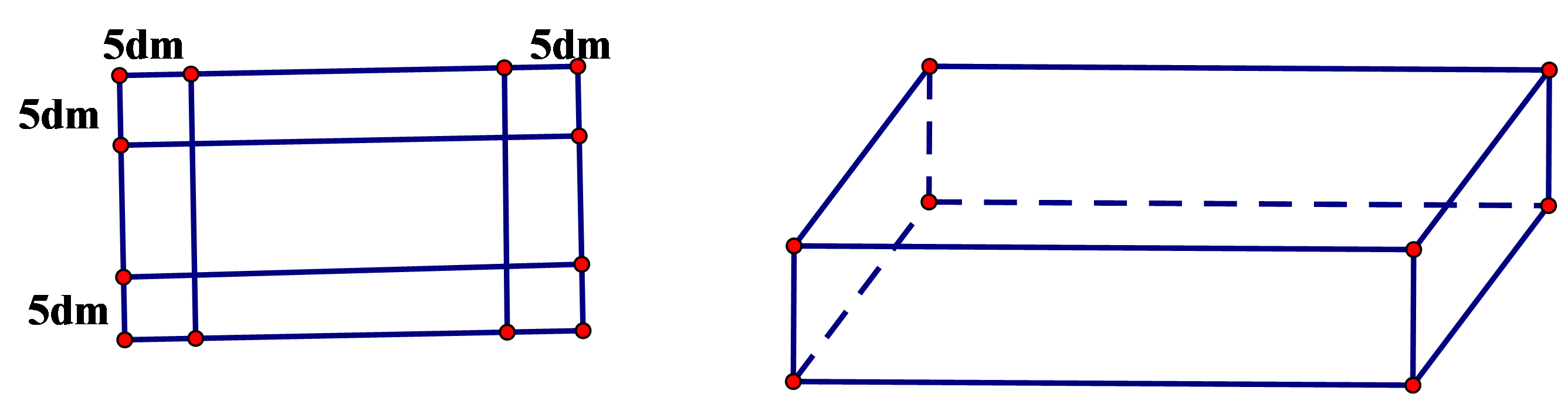
Gọi chiều rộng của miếng tôn lúc đầu là x (dm), \(x > 0\)

Chiều dài của nó là 2x (dm)

Khi làm thành một cái thùng không nắp thì chiều dài của thùng là \(2x - 10\) (dm), chiều rộng là \(x - 10\) (dm), chiều cao là 5dm.

Dung tích của thùng là \(5(2x - 10)(x - 10)(d{m^3})\)

Theo đầu bài ta có phương trình \(5(2x - 10)(x - 10) = 1500 \Leftrightarrow {x^2} - 15x - 100 = 0\)

Giải phương trình \(\Delta  = 225 + 400 = 625,\sqrt \Delta   = 25\)

Phương trình có nghiệm \({x_1} = 20,{x_2} =  - 5\) (loại)

Trả lời: Miếng tôn có chiều rộng bằng 20dm, chiều rộng bằng 40dm.