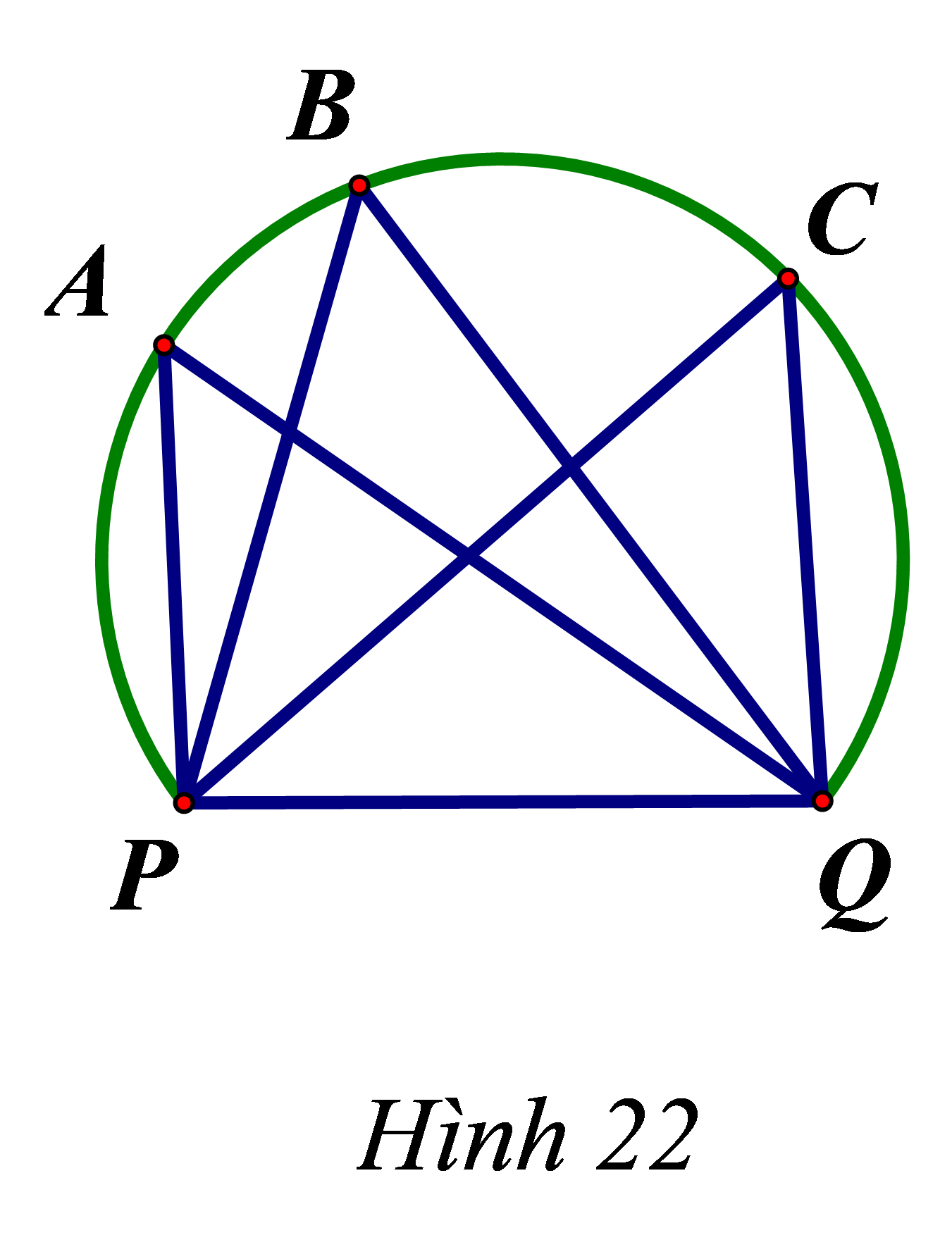
Một chiếc cầu được thiết kế như hình 30 có độ dài AB = 40m, chiều cao MK = 3m. Hãy tính bán kính của đường tròn chứa cung AMB.
Câu hỏi trong đề: 3 bài tập Toán thực tế (có lời giải) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
MK nằm trên đường kính MN của đường tròn, trong đó cung AMB là một cung của đường tròn đó.
Gọi bán kính của đường tròn là R thì \[KN = MN--MK = 2R--3.\]Vì MN \( \bot \) AB nên \[KA = KB = 20m\]
ta có:
\[KM.KN = KA.KB\], suy ra: 3.(2R – 3) =20.20 \( \Rightarrow R = \frac{{409}}{6} \approx 68,2(m)\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
\[\widehat {PAQ} = \widehat {PBQ} = \widehat {PCQ}\] (các góc nội tiếp cùng chắn cung PQ) .
Lời giải
Cung cả đường tròn là 360o, được chia làm 12 cung bằng nhau, mỗi cung có số đo là 30o.
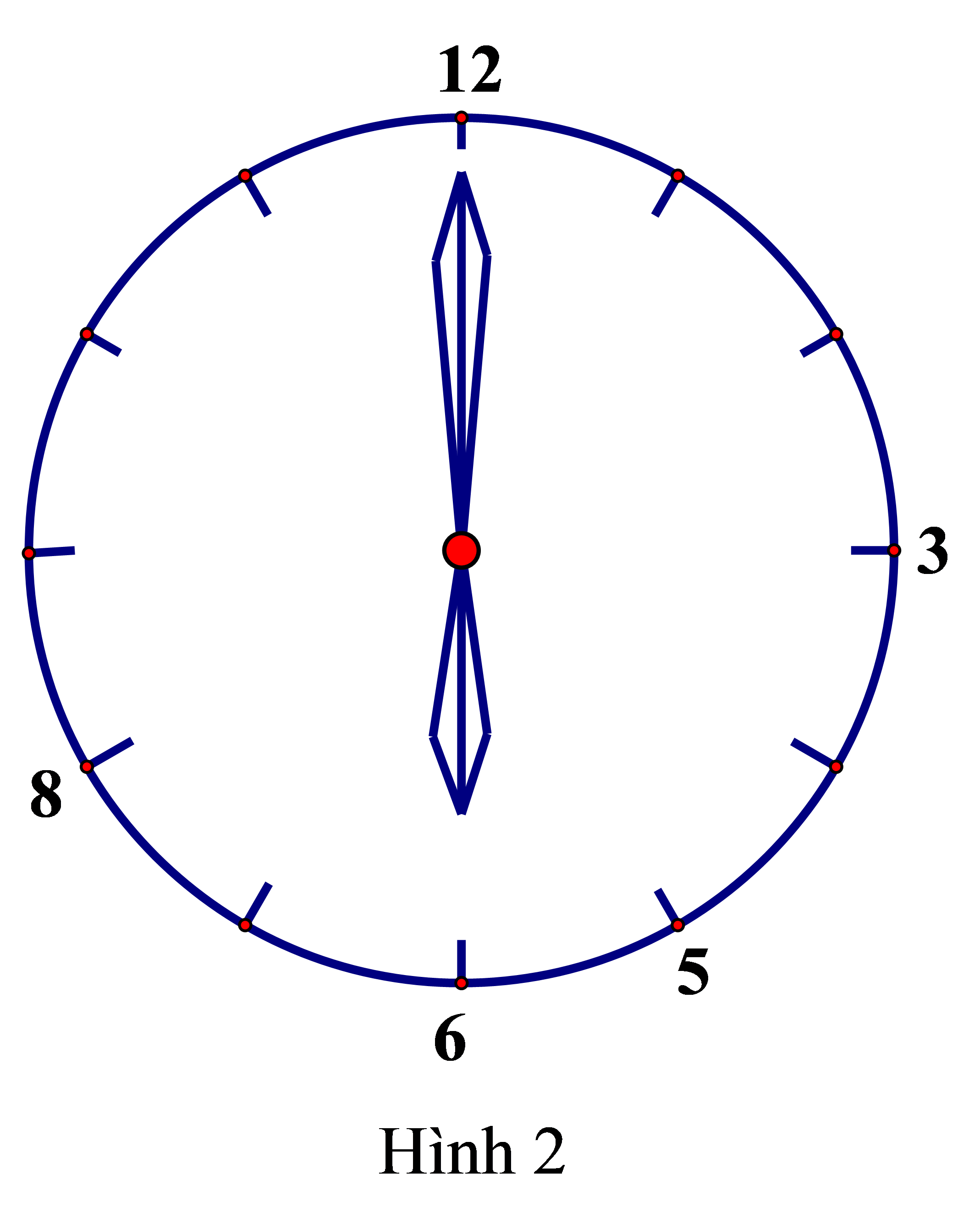
- Góc ở tâm lúc 3 giờ là \[30^\circ \cdot 3 = 90^\circ \];
- Góc ở tâm lúc 5 giờ là \[30^\circ \cdot 5 = 150^\circ \];
- Góc ở tâm lúc 6 giờ là \[30^\circ \cdot 6 = 180^\circ \];
- Góc ở tâm lúc 20 giờ là \[30^\circ \cdot 4 = 120^\circ \];
Nhắn tin Zalo
Hỏi bài tập