Cho tam giác \(ABC\) có ba góc nhọn. Vẽ các đường cao \(BD\) và \(CE\) của tam giác \(ABC\). Gọi \(H\) là giao điểm của \(BD\) và \(CE\).
a) Chứng minh \(ADHE\) là tứ giác nội tiếp.
b) Chứng minh \(BCDE\) là tứ giác nội tiếp.
Cho tam giác \(ABC\) có ba góc nhọn. Vẽ các đường cao \(BD\) và \(CE\) của tam giác \(ABC\). Gọi \(H\) là giao điểm của \(BD\) và \(CE\).
a) Chứng minh \(ADHE\) là tứ giác nội tiếp.
b) Chứng minh \(BCDE\) là tứ giác nội tiếp.
Quảng cáo
Trả lời:
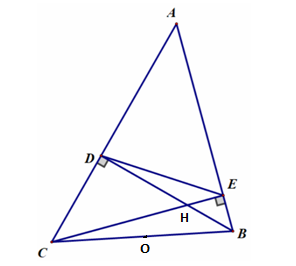
a) Chứng minh \[ADHE\] là tứ giác nội tiếp.
Vì \(BD,CE\) là các đường cao của \(\Delta ABC\) nên \(\left\{ {\begin{array}{*{20}{l}}{BD \bot AC}\\{CE \bot AB}\end{array}} \right. \Rightarrow \widehat {AEH} = \widehat {ADH} = {90^ \circ }\).
Xét tứ giác \(ADHE\) có \(\widehat {AEH} + \widehat {ADH} = {90^ \circ } + {90^ \circ } = {180^ \circ }\).
\[ \Rightarrow ADHE\] là tứ giác nội tiếp (Tứ giác có tổng 2 góc đối bằng \[{180^0}\]).
b) Chứng minh \(BCDE\) là tứ giác nội tiếp.
Gọi \(O\) là trung điểm\[BC\].
Vì \(BD,CE\) là các đường cao của \(\Delta ABC\) nên\(\left\{ {\begin{array}{*{20}{l}}{BD \bot AC}\\{CE \bot AB}\end{array} \Rightarrow \widehat {BDC} = \widehat {BEC} = {{90}^ \circ }} \right.\)
Xét tam giác \[BDC\] có \[\widehat {BDC} = {90^0}\] và \[DO\] là đường trung tuyến nên \[OD = OC = OB = \frac{1}{2}BC\] \[\left( 1 \right)\]
Xét tam giác \[BEC\] có \[\widehat {BEC} = {90^0}\] và \[EO\] là đường trung tuyến nên \[OE = OC = OB = \frac{1}{2}BC\] \[\left( 2 \right)\]
Từ \[\left( 1 \right)\]và \[\left( 2 \right)\] suy ra \[OD = OE = OC = OB\]
Vậy tứ giác \(BCDE\) nội tiếp được đường tròn có tâm \(O\) là trung điểm\[BC\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
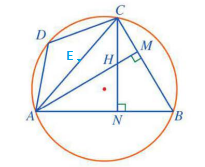
a) Chứng minh \(\widehat {ABC} = \widehat {CHM}\).
Vì \(AM,CN\) là các đường cao của \(\Delta ABC\) nên \(\left\{ {\begin{array}{*{20}{l}}{AM \bot BC}\\{CN \bot AB}\end{array}} \right. \Rightarrow \widehat {BMH} = \widehat {BNH} = {90^ \circ }\).
Xét tứ giác \(BNHM\) có \(\widehat {BMH} + \widehat {BNH} = {90^ \circ } + {90^ \circ } = {180^ \circ }\).
\( \Rightarrow BNHM\) là tứ giác nội tiếp (Tứ giác có tổng 2 góc đối bằng \[{180^0}\]).
Tứ giác \(BNHM\) nội tiếp nên: \(\widehat {MBN} + \widehat {NHM} = {180^ \circ }\) hay \(\widehat {CBA} + \widehat {NHM} = {180^ \circ }\)
mà \(\widehat {MBN} + \widehat {NHM} = {180^ \circ }\) (hai góc kề bù)
do đó \(\widehat {CBA} = \widehat {MBN}\)
b) Chứng minh \(\widehat {ADC} = \widehat {AHC}\).
Tứ giác \(BNHM\) nội tiếp nên: \(\widehat {MBN} + \widehat {NHM} = {180^ \circ }\)
mà\(\widehat {AHC} = \widehat {NHM}\) (đối đỉnh)
nên \(\widehat {MBN} + \widehat {AHC} = {180^ \circ }\)
hay \(\widehat {ABC} + \widehat {AHC} = {180^ \circ }\)
Mặc khác tứ giác \(BNHM\) nội tiếp đường tròn tâm \(\left( O \right)\) nên \(\widehat {ADC} + \widehat {ABC} = {180^0}\)
Do đó \(\widehat {ADC} = \widehat {AHC}\)
c) Chứng minh \(\widehat {MAC} = \widehat {MNC}\).
Ta chứng minh \(ACMN\) là tứ giác nội tiếp.
Gọi \(E\) là trung điểm\[AC\].
Xét tam giác \[AMC\] có \[\widehat {AMC} = {90^0}\] và \[ME\] là đường trung tuyến nên \[EM = EC = EA = \frac{1}{2}AC\] \[\left( 1 \right)\]
Xét tam giác \[ANC\] có \[\widehat {ANC} = {90^0}\] và \[NE\] là đường trung tuyến nên \[EN = EC = EA = \frac{1}{2}AC\] \[\left( 2 \right)\]
Từ \[\left( 1 \right)\]và \[\left( 2 \right)\] suy ra \[EM = EN = EC = EA\]
Vậy tứ giác \(ACMN\) nội tiếp được đường tròn có tâm \(E\) là trung điểm\[AC\].
Suy ra \(\widehat {MAC} = \widehat {MNC}\) (góc nội tiếp cùng chắn cung \[MC\] của đường tròn tâm \(E\))
d) Chứng minh \(\widehat {MAC} + {90^0} = \widehat {ANM}\).
Ta có \(\widehat {MAC} + \widehat {ACM} = {90^0}\) (hai góc phụ nhau)
Hay \(\widehat {ACM} = {90^0} - \widehat {MAC}\)
Mà \(\widehat {ACM} + \widehat {ANM} = {180^0}\) ( tứ giác \(ACMN\) nội tiếp được đường tròn, câu c))
Nên \({90^0} - \widehat {MAC} + \widehat {ANM} = {180^0}\)
Suy ra \(\widehat {MAC} + {90^0} = \widehat {ANM}\)
Lời giải
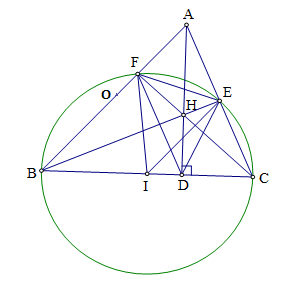
a) Chứng minh tứ giác \(BFHD\) nội tiếp.
- Xét đường tròn \(\left( I \right)\)
\(\widehat {CFB} = {90^0}\)(góc nội tiếp chắn nửa đường tròn) \( \Rightarrow CF \bot AB\)
\(\widehat {CFB} = {90^0}\)(góc nội tiếp chắn nửa đường tròn) \( \Rightarrow BE \bot AC\)
Suy ra \(H\) là trực tâm của tam giác\(ABC\) hay \(AH \bot BC \Rightarrow \)\(\widehat {HDB} = {90^0}\)
- Xét tứ giác \(BFHD\)
\(\widehat {CFB} = \widehat {HDB} = {90^0}\)(chứng minh trên)
\( \Rightarrow \widehat {CFB} + \widehat {HDB} = {180^0}\)
tứ giác \(BFHD\) có tổng hai góc đối \(\widehat {CFB},\widehat {HDB}\) bằng \({180^0}\) nên tứ giác \(BFHD\) nội tiếp.
b) Chứng minh tứ giác \(ABDE\) nội tiếp.
Gọi \(O\) là trung điểm\[AB\].
Xét tam giác \[ADB\] có \[\widehat {ADB} = {90^0}\] và \[DO\] là đường trung tuyến nên \[OD = OA = OB = \frac{1}{2}AB\] \[\left( 1 \right)\]
Xét tam giác \[AEB\] có \[\widehat {AEB} = {90^0}\] và \[EO\] là đường trung tuyến nên \[OE = OA = OB = \frac{1}{2}AB\] \[\left( 2 \right)\]
Từ \[\left( 1 \right)\]và \[\left( 2 \right)\] suy ra \[OD = OE = OA = OB\]
Vậy tứ giác \(ABDE\) nội tiếp được đường tròn có tâm \(O\) là trung điểm\[AB\].