3 bài tập Chứng minh tứ giác nội tiếp đường tròn (có lời giải)

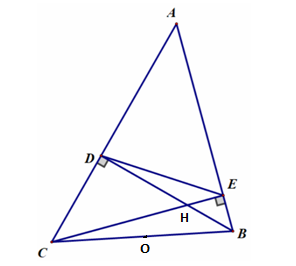
a) Chứng minh \[ADHE\] là tứ giác nội tiếp.

Vì \(BD,CE\) là các đường cao của \(\Delta ABC\) nên \(\left\{ {\begin{array}{*{20}{l}}{BD \bot AC}\\{CE \bot AB}\end{array}} \right. \Rightarrow \widehat {AEH} = \widehat {ADH} = {90^ \circ }\).

Xét tứ giác \(ADHE\) có \(\widehat {AEH} + \widehat {ADH} = {90^ \circ } + {90^ \circ } = {180^ \circ }\).

\[ \Rightarrow ADHE\] là tứ giác nội tiếp (Tứ giác có tổng 2 góc đối bằng \[{180^0}\]).

b) Chứng minh \(BCDE\) là tứ giác nội tiếp.

Gọi  \(O\) là trung điểm\[BC\].

Vì \(BD,CE\) là các đường cao của \(\Delta ABC\) nên\(\left\{ {\begin{array}{*{20}{l}}{BD \bot AC}\\{CE \bot AB}\end{array} \Rightarrow \widehat {BDC} = \widehat {BEC} = {{90}^ \circ }} \right.\)

Xét tam giác \[BDC\] có \[\widehat {BDC} = {90^0}\] và \[DO\] là đường trung tuyến nên \[OD = OC = OB = \frac{1}{2}BC\] \[\left( 1 \right)\]

Xét tam giác \[BEC\] có \[\widehat {BEC} = {90^0}\] và \[EO\] là đường trung tuyến nên \[OE = OC = OB = \frac{1}{2}BC\] \[\left( 2 \right)\]

Từ \[\left( 1 \right)\]và \[\left( 2 \right)\] suy ra \[OD = OE = OC = OB\]

Vậy tứ giác \(BCDE\) nội tiếp được đường tròn có tâm \(O\) là trung điểm\[BC\].

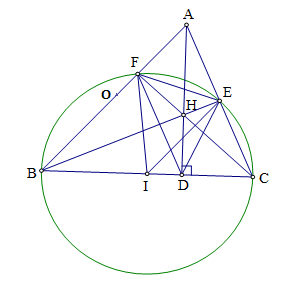
a) Chứng minh tứ giác \(BFHD\) nội tiếp.

- Xét đường tròn \(\left( I \right)\)

     \(\widehat {CFB} = {90^0}\)(góc nội tiếp chắn nửa đường tròn) \( \Rightarrow CF \bot AB\)

     \(\widehat {CFB} = {90^0}\)(góc nội tiếp chắn nửa đường tròn) \( \Rightarrow BE \bot AC\)

     Suy ra \(H\) là trực tâm của tam giác\(ABC\) hay \(AH \bot BC \Rightarrow \)\(\widehat {HDB} = {90^0}\)

- Xét tứ giác \(BFHD\)

     \(\widehat {CFB} = \widehat {HDB} = {90^0}\)(chứng minh trên)

     \( \Rightarrow \widehat {CFB} + \widehat {HDB} = {180^0}\)

tứ giác \(BFHD\) có tổng hai góc đối \(\widehat {CFB},\widehat {HDB}\) bằng \({180^0}\) nên tứ giác \(BFHD\) nội tiếp.

b)  Chứng minh tứ giác \(ABDE\) nội tiếp.

Gọi  \(O\) là trung điểm\[AB\].

Xét tam giác \[ADB\] có \[\widehat {ADB} = {90^0}\] và \[DO\] là đường trung tuyến nên \[OD = OA = OB = \frac{1}{2}AB\] \[\left( 1 \right)\]

Xét tam giác \[AEB\] có \[\widehat {AEB} = {90^0}\] và \[EO\] là đường trung tuyến nên \[OE = OA = OB = \frac{1}{2}AB\] \[\left( 2 \right)\]

Từ \[\left( 1 \right)\]và \[\left( 2 \right)\] suy ra \[OD = OE = OA = OB\]

Vậy tứ giác \(ABDE\) nội tiếp được đường tròn có tâm \(O\) là trung điểm\[AB\].

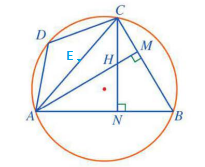
a) Chứng minh \(\widehat {ABC} = \widehat {CHM}\).

Vì \(AM,CN\) là các đường cao của \(\Delta ABC\) nên \(\left\{ {\begin{array}{*{20}{l}}{AM \bot BC}\\{CN \bot AB}\end{array}} \right. \Rightarrow \widehat {BMH} = \widehat {BNH} = {90^ \circ }\).

Xét tứ giác \(BNHM\) có \(\widehat {BMH} + \widehat {BNH} = {90^ \circ } + {90^ \circ } = {180^ \circ }\).

\( \Rightarrow BNHM\) là tứ giác nội tiếp (Tứ giác có tổng 2 góc đối bằng \[{180^0}\]).

Tứ giác \(BNHM\) nội tiếp nên: \(\widehat {MBN} + \widehat {NHM} = {180^ \circ }\) hay \(\widehat {CBA} + \widehat {NHM} = {180^ \circ }\)

mà \(\widehat {MBN} + \widehat {NHM} = {180^ \circ }\) (hai góc kề bù)

do đó \(\widehat {CBA} = \widehat {MBN}\)

b) Chứng minh \(\widehat {ADC} = \widehat {AHC}\).

Tứ giác \(BNHM\) nội tiếp nên: \(\widehat {MBN} + \widehat {NHM} = {180^ \circ }\)

mà\(\widehat {AHC} = \widehat {NHM}\) (đối đỉnh)

nên \(\widehat {MBN} + \widehat {AHC} = {180^ \circ }\)

hay \(\widehat {ABC} + \widehat {AHC} = {180^ \circ }\)

Mặc khác tứ giác \(BNHM\) nội tiếp đường tròn tâm \(\left( O \right)\) nên \(\widehat {ADC} + \widehat {ABC} = {180^0}\)

Do đó \(\widehat {ADC} = \widehat {AHC}\)

c) Chứng minh \(\widehat {MAC} = \widehat {MNC}\).

Ta chứng minh \(ACMN\) là tứ giác nội tiếp.

Gọi  \(E\) là trung điểm\[AC\].

Xét tam giác \[AMC\] có \[\widehat {AMC} = {90^0}\] và \[ME\] là đường trung tuyến nên \[EM = EC = EA = \frac{1}{2}AC\] \[\left( 1 \right)\]

Xét tam giác \[ANC\] có \[\widehat {ANC} = {90^0}\] và \[NE\] là đường trung tuyến nên \[EN = EC = EA = \frac{1}{2}AC\] \[\left( 2 \right)\]

Từ \[\left( 1 \right)\]và \[\left( 2 \right)\] suy ra \[EM = EN = EC = EA\]

Vậy tứ giác \(ACMN\) nội tiếp được đường tròn có tâm \(E\) là trung điểm\[AC\].

Suy ra \(\widehat {MAC} = \widehat {MNC}\) (góc nội tiếp cùng chắn cung \[MC\] của đường tròn tâm \(E\))

d) Chứng minh \(\widehat {MAC} + {90^0} = \widehat {ANM}\).

Ta có \(\widehat {MAC} + \widehat {ACM} = {90^0}\) (hai góc phụ nhau)

Hay \(\widehat {ACM} = {90^0} - \widehat {MAC}\)

Mà \(\widehat {ACM} + \widehat {ANM} = {180^0}\) ( tứ giác \(ACMN\) nội tiếp được đường tròn, câu c))

Nên \({90^0} - \widehat {MAC} + \widehat {ANM} = {180^0}\)

Suy ra \(\widehat {MAC} + {90^0} = \widehat {ANM}\)