Cho tam giác\(ABC\) có ba góc nhọn, \(AB < AC\) và nội tiếp đường tròn \(\left( O \right)\). Gọi \(BE\), \(CF\) là các đường cao và \(H\) là trực tâm của tam giác \(ABC\).
a) Chứng minh tứ giác \(AEHF\) là tứ giác nội tiếp.
b) Đường tròn ngoại tiếp tứ giác \(AEHF\) cắt đường tròn \[\left( O \right)\] tại điểm thứ hai \[I\] (\[A\] không trùng với \[I\]). Chứng minh hai tam giác \[IBC\] và \[IFE\] đồng dạng với nhau.
c) Hai đường thẳng \[BC\] và \[EF\] cắt nhau tại \[K\]. Chứng minh ba điểm \[A,{\rm{ }}I,{\rm{ }}K\]thẳng hàng.
Cho tam giác\(ABC\) có ba góc nhọn, \(AB < AC\) và nội tiếp đường tròn \(\left( O \right)\). Gọi \(BE\), \(CF\) là các đường cao và \(H\) là trực tâm của tam giác \(ABC\).
a) Chứng minh tứ giác \(AEHF\) là tứ giác nội tiếp.
b) Đường tròn ngoại tiếp tứ giác \(AEHF\) cắt đường tròn \[\left( O \right)\] tại điểm thứ hai \[I\] (\[A\] không trùng với \[I\]). Chứng minh hai tam giác \[IBC\] và \[IFE\] đồng dạng với nhau.
c) Hai đường thẳng \[BC\] và \[EF\] cắt nhau tại \[K\]. Chứng minh ba điểm \[A,{\rm{ }}I,{\rm{ }}K\]thẳng hàng.
Quảng cáo
Trả lời:
Giải bởi Vietjack
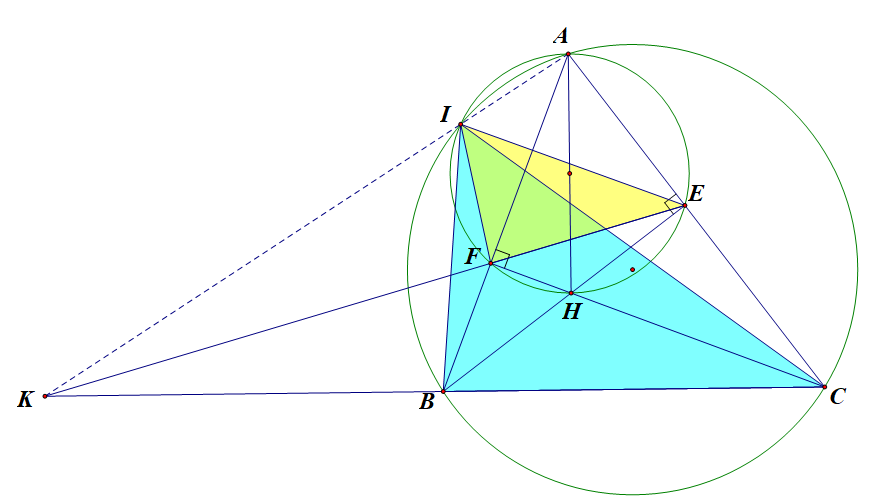
a) Xét tứ giác \(AEHF\), ta có: \(\widehat {AFH} = 90^\circ \)(Vì CF là đường cao của tam giác ABC)
\(\widehat {AEH} = 90^\circ \)( Vì BE là đường cao của tam giác ABC)
Do đó \[\widehat {AFH} + \widehat {AEH} = 90^\circ + 90^\circ = 180^\circ \]
Vậy tứ giác \(AEHF\)là tứ giác nội tiếp .
b) Xét tứ giác \(AEHF\), ta có: \(\widehat {IEF} = \widehat {IAF}\)(cùng chắn )
\(\widehat {IAF} = \widehat {IBC}\) (cùng chắn )
Do đó \(\widehat {IEF} = \widehat {IBC}\)
Tương tự, \(\widehat {FIE} = \widehat {FAE}\) (cùng chắn )
\(\widehat {FAE} = \widehat {BIC}\)(cùng chắn )
Do đó \(\widehat {FIE} = \widehat {BIC}\)
Xét \(\Delta IBC\) và \(\Delta IFE\), ta có: \(\widehat {IEF} = \widehat {IBC}\)(cmt)
\(\widehat {FIE} = \widehat {BIC}\)(cmt)
Do đó
c)
Tứ giác \(IAEF\) nội tiếp \( \Rightarrow \widehat {IFK} = \widehat {IAE}\)
Tứ giác \(IABC\) nội tiếp \( \Rightarrow \widehat {IBK} = \widehat {IAE}\)
Suy ra \(\widehat {IFK} = \widehat {IBK}\)
Suy ra tứ giác \(IFBK\) nội tiếp (có hai đỉnh \(B,F\) kề cùng nhìn cạnh \(IK\) dưới một góc bằng nhau).
Vậy \(\widehat {KIF} + \widehat {KBF} = 180^\circ \), mà \(\widehat {KBF} = \widehat {FEC} = \widehat {FIA}\)
\( \Rightarrow \widehat {KIF} + \widehat {FIA} = 180^\circ \) hay ba điểm \[A,{\rm{ }}I,{\rm{ }}K\]thẳng hàng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
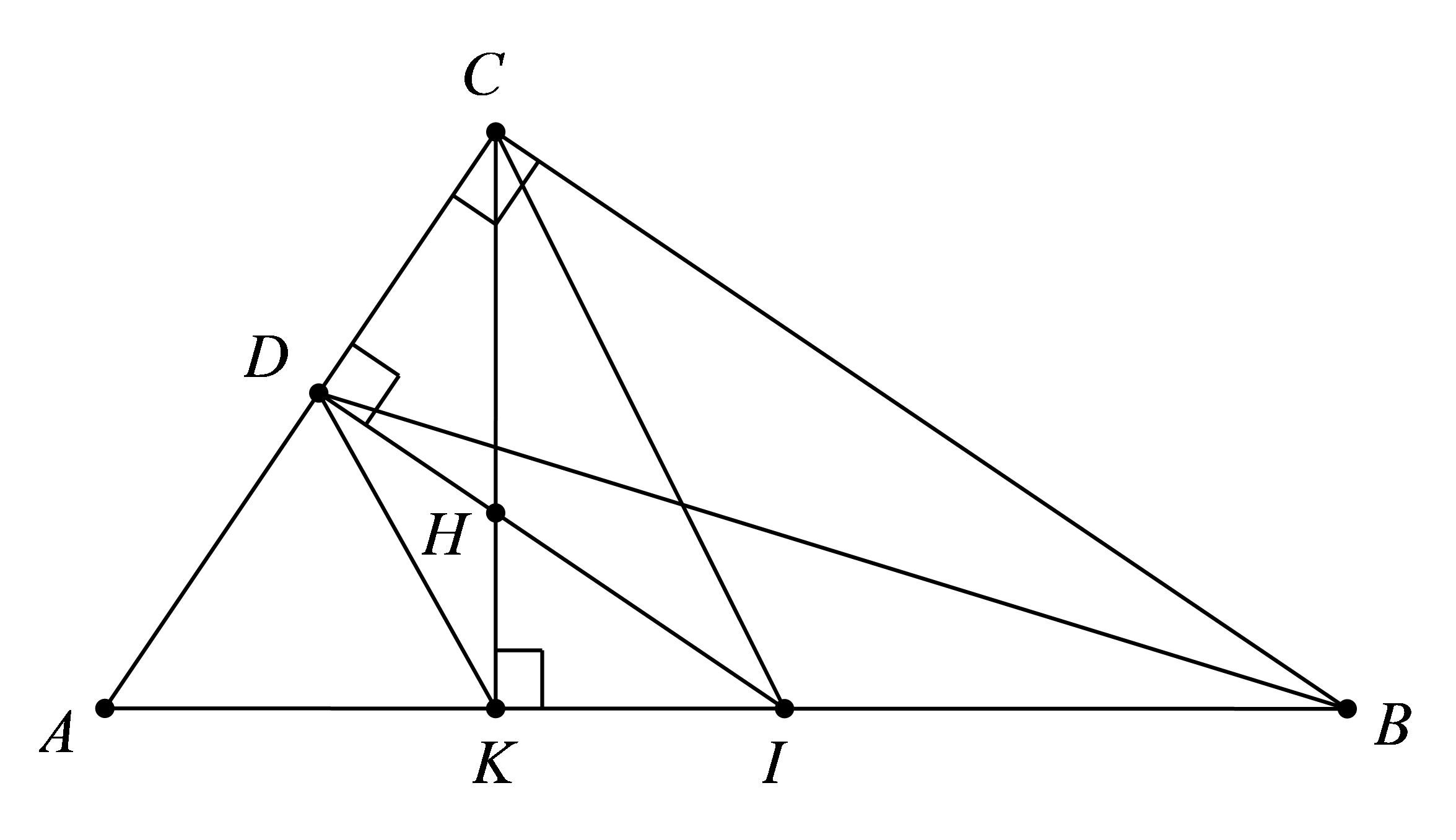
a) Ta có : \(\widehat {CDI} = {90^0}\) (gt)
\(\widehat {CKI} = {90^0}\) (gt)
\( \Rightarrow \widehat {CDI} = \widehat {CKI}\)
Vậy tứ giác CDKI nội tiếp.
b) Ta có: BD là phân giác của tam giác ABC (gt) \( \Rightarrow \frac{{AD}}{{DC}} = \frac{{AB}}{{BC}} \Rightarrow \frac{{AD}}{{AB}} = \frac{{DC}}{{BC}}\) (1)
Xét \(\Delta DCH\) và \(\Delta CBA\) có:
\(\widehat {CDH} = \widehat {BCA}\;\;\left( { = {{90}^0}} \right)\)
\(\widehat {DCH} = \widehat {CBA}\) (cùng phụ \(\widehat {BAC}\))
\( \Rightarrow \Delta DCH \sim \Delta CBA\) (g-g)
\( \Rightarrow \frac{{DH}}{{AC}} = \frac{{DC}}{{BC}}\) (2)
Từ (1), (2) \( \Rightarrow \frac{{DH}}{{AC}} = \frac{{AD}}{{AB}} \Rightarrow AC.AD = AB.DH\)
c)
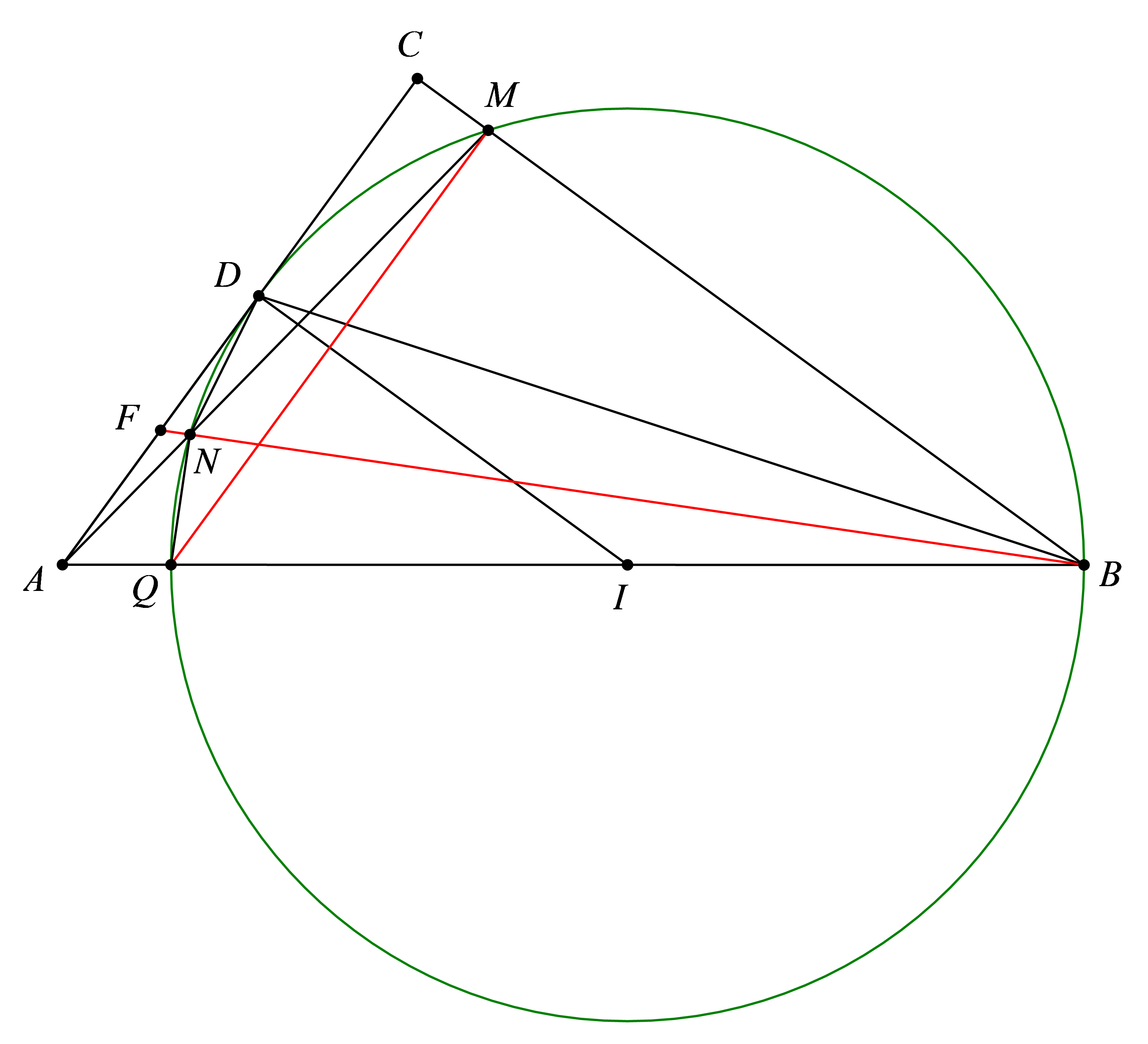
Gọi F’ là giao điểm của BN với AD, Q là giao điểm của AB với (I).
Ta có: ID // BC (cùng vuông góc với AC) \( \Rightarrow \widehat {IDB} = \widehat {DBC}\)
Mà \(\widehat {DBI} = \widehat {DBC}\) (gt)
\( \Rightarrow \widehat {IDB} = \widehat {DBI}\)
\( \Rightarrow \Delta IDB\)cân tại I \( \Rightarrow IB = ID \Rightarrow B \in (I)\)
\( \Rightarrow \) tứ giác BMNQ nội tiếp
\( \Rightarrow \widehat {NBQ} = \widehat {NMQ}\)
Ta có: \(\widehat {QMB} = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow QM \bot BC\)
\( \Rightarrow \) QM // AC (cùng vuông góc với BC)
\( \Rightarrow \widehat {NMQ} = \widehat {MAD}\) (so le trong)
\( \Rightarrow \widehat {NAF'} = \widehat {F'BA}\)
Xét \(\Delta F'AN\) và \(\Delta F'BA\) có:
\(\widehat {NAF'} = \widehat {F'BA}\) (c/m trên)
\(\widehat {BF'A}\) chung
\( \Rightarrow \) \(\Delta F'AN\) \( \sim \) \(\Delta F'BA\) (g-g)
\( \Rightarrow \frac{{F'A}}{{F'B}} = \frac{{F'N}}{{F'A}} \Rightarrow F'{A^2} = F'B.F'N\) (3)
Ta lại có: \(DA \bot ID\) (gt) nên DA là tiếp tuyến của (I) \( \Rightarrow \widehat {F'DN} = \widehat {NBD}\)
Xét \(\Delta F'DN\) và \(\Delta F'BD\) có:
\(\widehat {F'DN} = \widehat {NBD}\) (c/m trên)
\(\widehat {BF'D}\) chung
\( \Rightarrow \) \(\Delta F'DN\) \( \sim \) \(\Delta F'BD\) (g-g)
\( \Rightarrow \frac{{F'D}}{{F'B}} = \frac{{F'N}}{{F'D}} \Rightarrow F'{D^2} = F'B.F'N\) (4)
Từ (3), (4) \( \Rightarrow F'{A^2} = F'{D^2}\) \( \Rightarrow \) F’A = F’D Hay F’ là trung điểm của AD
Do đó F’ trùng với F
Vậy F, N, B thẳng hàng
Nhắn tin Zalo
Hỏi bài tập