Cho tam giác ABC vuông tại C (AC < BC), đường cao CK và đường phân giác BD \(\left( {K \in AB,\;D \in AC} \right)\). Qua D kẻ đường thẳng vuông góc với AC cắt CK, AB lần lượt tại H và I.
a) Chứng minh tứ giác CDKI nội tiếp.
b) Chứng minh AC.AD = DH.AB.
c) Gọi F là trung điểm của AD. Đường tròn tâm I bán kính ID cắt BC tại M ( M khác B) và cắt AM tại N (N khác M). Chứng minh B, N, F thẳng hàng.
Cho tam giác ABC vuông tại C (AC < BC), đường cao CK và đường phân giác BD \(\left( {K \in AB,\;D \in AC} \right)\). Qua D kẻ đường thẳng vuông góc với AC cắt CK, AB lần lượt tại H và I.
a) Chứng minh tứ giác CDKI nội tiếp.
b) Chứng minh AC.AD = DH.AB.
c) Gọi F là trung điểm của AD. Đường tròn tâm I bán kính ID cắt BC tại M ( M khác B) và cắt AM tại N (N khác M). Chứng minh B, N, F thẳng hàng.
Quảng cáo
Trả lời:
Giải bởi Vietjack
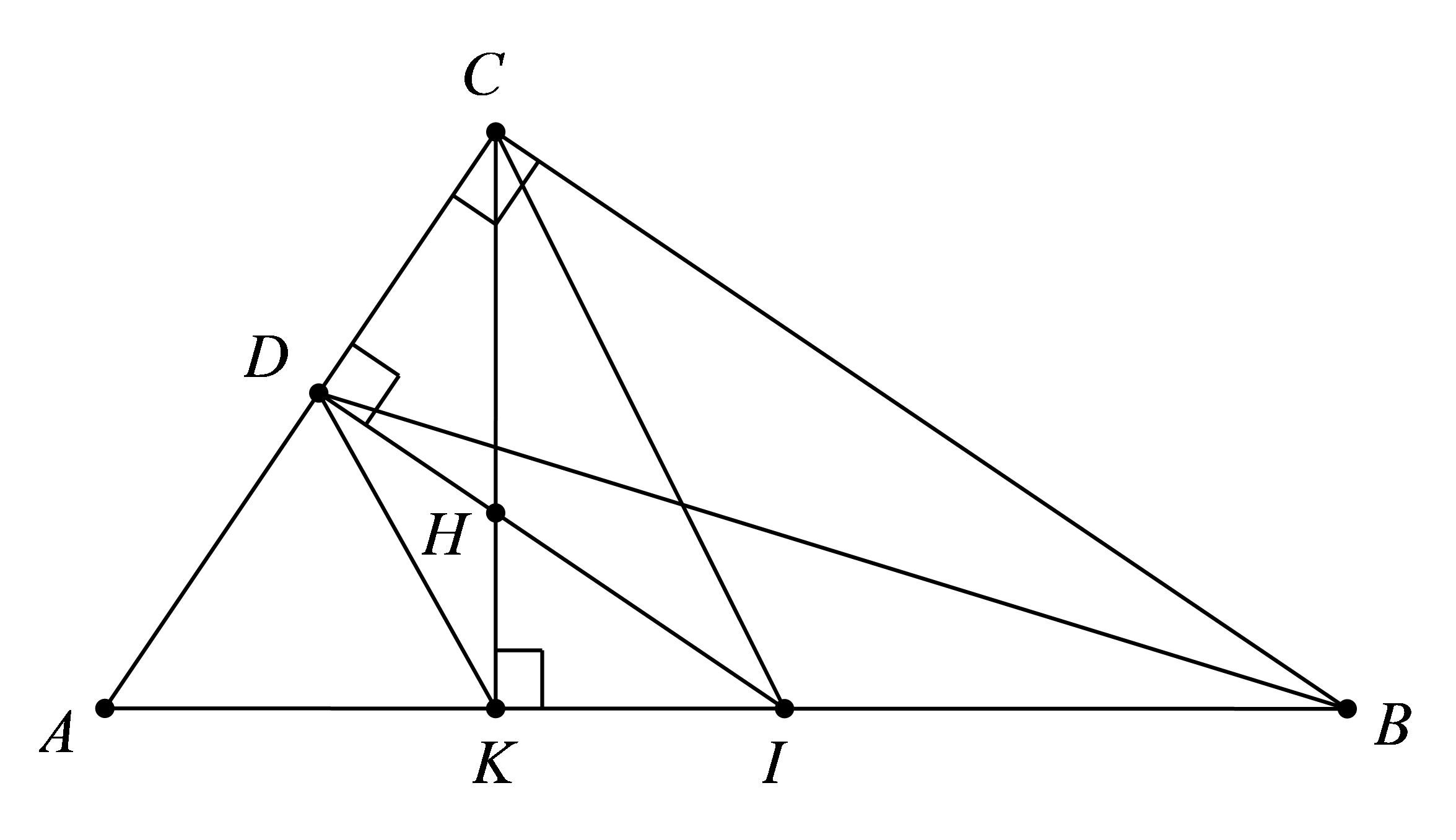
a) Ta có : \(\widehat {CDI} = {90^0}\) (gt)
\(\widehat {CKI} = {90^0}\) (gt)
\( \Rightarrow \widehat {CDI} = \widehat {CKI}\)
Vậy tứ giác CDKI nội tiếp.
b) Ta có: BD là phân giác của tam giác ABC (gt) \( \Rightarrow \frac{{AD}}{{DC}} = \frac{{AB}}{{BC}} \Rightarrow \frac{{AD}}{{AB}} = \frac{{DC}}{{BC}}\) (1)
Xét \(\Delta DCH\) và \(\Delta CBA\) có:
\(\widehat {CDH} = \widehat {BCA}\;\;\left( { = {{90}^0}} \right)\)
\(\widehat {DCH} = \widehat {CBA}\) (cùng phụ \(\widehat {BAC}\))
\( \Rightarrow \Delta DCH \sim \Delta CBA\) (g-g)
\( \Rightarrow \frac{{DH}}{{AC}} = \frac{{DC}}{{BC}}\) (2)
Từ (1), (2) \( \Rightarrow \frac{{DH}}{{AC}} = \frac{{AD}}{{AB}} \Rightarrow AC.AD = AB.DH\)
c)
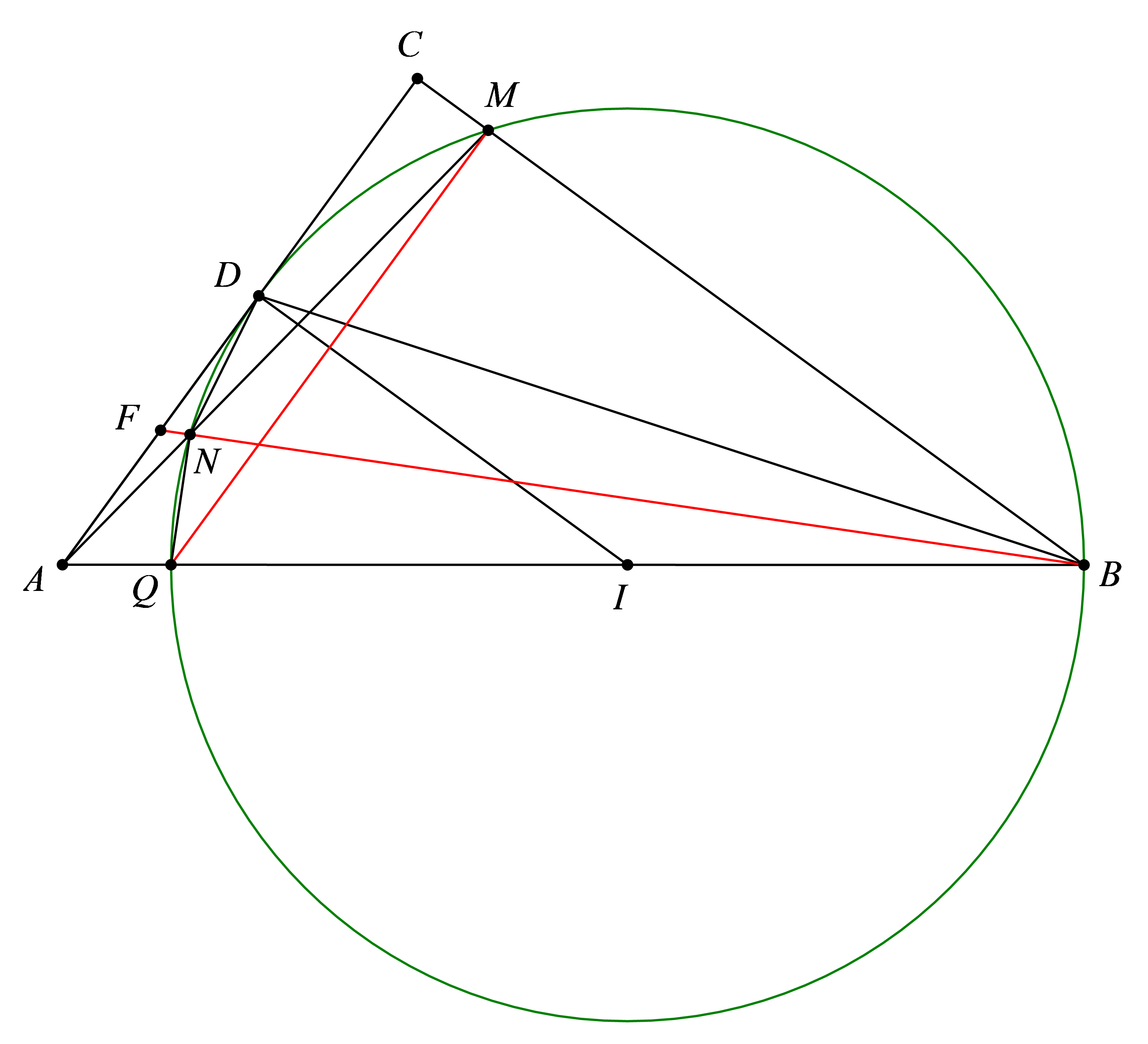
Gọi F’ là giao điểm của BN với AD, Q là giao điểm của AB với (I).
Ta có: ID // BC (cùng vuông góc với AC) \( \Rightarrow \widehat {IDB} = \widehat {DBC}\)
Mà \(\widehat {DBI} = \widehat {DBC}\) (gt)
\( \Rightarrow \widehat {IDB} = \widehat {DBI}\)
\( \Rightarrow \Delta IDB\)cân tại I \( \Rightarrow IB = ID \Rightarrow B \in (I)\)
\( \Rightarrow \) tứ giác BMNQ nội tiếp
\( \Rightarrow \widehat {NBQ} = \widehat {NMQ}\)
Ta có: \(\widehat {QMB} = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow QM \bot BC\)
\( \Rightarrow \) QM // AC (cùng vuông góc với BC)
\( \Rightarrow \widehat {NMQ} = \widehat {MAD}\) (so le trong)
\( \Rightarrow \widehat {NAF'} = \widehat {F'BA}\)
Xét \(\Delta F'AN\) và \(\Delta F'BA\) có:
\(\widehat {NAF'} = \widehat {F'BA}\) (c/m trên)
\(\widehat {BF'A}\) chung
\( \Rightarrow \) \(\Delta F'AN\) \( \sim \) \(\Delta F'BA\) (g-g)
\( \Rightarrow \frac{{F'A}}{{F'B}} = \frac{{F'N}}{{F'A}} \Rightarrow F'{A^2} = F'B.F'N\) (3)
Ta lại có: \(DA \bot ID\) (gt) nên DA là tiếp tuyến của (I) \( \Rightarrow \widehat {F'DN} = \widehat {NBD}\)
Xét \(\Delta F'DN\) và \(\Delta F'BD\) có:
\(\widehat {F'DN} = \widehat {NBD}\) (c/m trên)
\(\widehat {BF'D}\) chung
\( \Rightarrow \) \(\Delta F'DN\) \( \sim \) \(\Delta F'BD\) (g-g)
\( \Rightarrow \frac{{F'D}}{{F'B}} = \frac{{F'N}}{{F'D}} \Rightarrow F'{D^2} = F'B.F'N\) (4)
Từ (3), (4) \( \Rightarrow F'{A^2} = F'{D^2}\) \( \Rightarrow \) F’A = F’D Hay F’ là trung điểm của AD
Do đó F’ trùng với F
Vậy F, N, B thẳng hàng
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
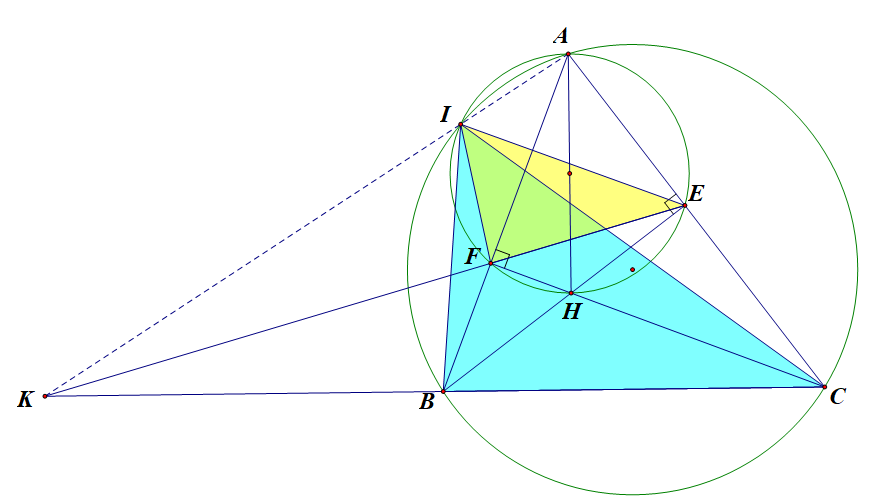
a) Xét tứ giác \(AEHF\), ta có: \(\widehat {AFH} = 90^\circ \)(Vì CF là đường cao của tam giác ABC)
\(\widehat {AEH} = 90^\circ \)( Vì BE là đường cao của tam giác ABC)
Do đó \[\widehat {AFH} + \widehat {AEH} = 90^\circ + 90^\circ = 180^\circ \]
Vậy tứ giác \(AEHF\)là tứ giác nội tiếp .
b) Xét tứ giác \(AEHF\), ta có: \(\widehat {IEF} = \widehat {IAF}\)(cùng chắn )
\(\widehat {IAF} = \widehat {IBC}\) (cùng chắn )
Do đó \(\widehat {IEF} = \widehat {IBC}\)
Tương tự, \(\widehat {FIE} = \widehat {FAE}\) (cùng chắn )
\(\widehat {FAE} = \widehat {BIC}\)(cùng chắn )
Do đó \(\widehat {FIE} = \widehat {BIC}\)
Xét \(\Delta IBC\) và \(\Delta IFE\), ta có: \(\widehat {IEF} = \widehat {IBC}\)(cmt)
\(\widehat {FIE} = \widehat {BIC}\)(cmt)
Do đó
c)
Tứ giác \(IAEF\) nội tiếp \( \Rightarrow \widehat {IFK} = \widehat {IAE}\)
Tứ giác \(IABC\) nội tiếp \( \Rightarrow \widehat {IBK} = \widehat {IAE}\)
Suy ra \(\widehat {IFK} = \widehat {IBK}\)
Suy ra tứ giác \(IFBK\) nội tiếp (có hai đỉnh \(B,F\) kề cùng nhìn cạnh \(IK\) dưới một góc bằng nhau).
Vậy \(\widehat {KIF} + \widehat {KBF} = 180^\circ \), mà \(\widehat {KBF} = \widehat {FEC} = \widehat {FIA}\)
\( \Rightarrow \widehat {KIF} + \widehat {FIA} = 180^\circ \) hay ba điểm \[A,{\rm{ }}I,{\rm{ }}K\]thẳng hàng.
Nhắn tin Zalo
Hỏi bài tập