Cho hình tròn \(\left( {O;R} \right)\).
a) Vẽ hình tam giác đều, hình vuông, hình lục giác đều có các đỉnh nằm trên \(\left( {O;R} \right)\).
b) Tính các cạnh của các hình vừa vẽ theo \(R\).
Cho hình tròn \(\left( {O;R} \right)\).
a) Vẽ hình tam giác đều, hình vuông, hình lục giác đều có các đỉnh nằm trên \(\left( {O;R} \right)\).
b) Tính các cạnh của các hình vừa vẽ theo \(R\).
Câu hỏi trong đề: Các dạng bài tập Đa giác đều lớp 9 (có lời giải) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
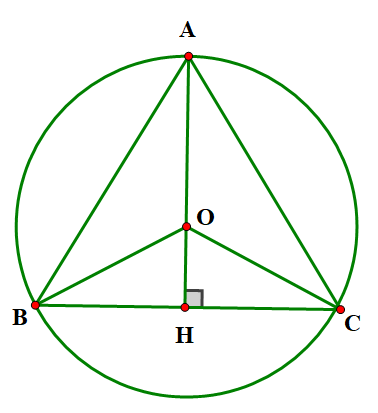
a) • Vẽ tam giác đều \(ABC\) nội tiếp đường tròn \(\left( {O;R} \right)\). Vẽ đường cao \(AH\), ta có:\(AB = AC;OB = OC = R\)
Nên \(A,O,H\) thuộc đường trung trực của \(BC\) vì đều nên \(O\) là trọng tâm của tam giác.
Ta có \(AH = \frac{3}{2}AO = \frac{3}{2}R{\rm{ }}(1)\) (tính chất trọng tâm). Lại có \(AH\) là đường cao của tam giác \(ABC\) đều nên \(AH = \frac{{AB\sqrt 3 }}{2}\). Từ (1) và (2) \( \Rightarrow \frac{3}{2}R = \frac{{AB\sqrt 3 }}{2} \Rightarrow AB = \frac{{3R}}{{\sqrt 3 }} = \sqrt 3 .R\)
Vậy cạnh của tam giác đều nội tiếp đường tròn \(\left( {O;R} \right)\) là \(\sqrt 3 {\rm{.R}}\).
- Vẽ hình vuông\(ABCD\) nội tiếp đường tròn \(\left( {O;R} \right)\).
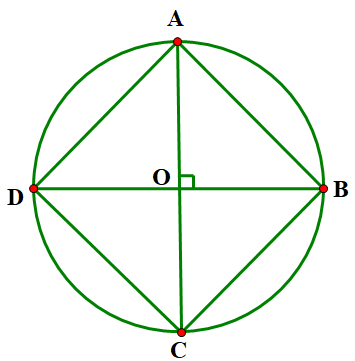
Ta có: \({\rm{AC}} \bot {\rm{BD}}\) (tính chất hai đường chéo hình vuông). Xét tam giác \(AOB\) vuông tại \(O\).
Theo định lí Pythgore, ta có:\(A{B^2} = O{A^2} + O{B^2} = {R^2} + {R^2} = 2{R^2} \Rightarrow AB = \sqrt {2{R^2}} = R\sqrt 2 \)
Vậy cạnh của hình vuông nội tiếp đường tròn \(\left( {O;R} \right)\) là \(R\sqrt 2 \).
- Vẽ lục giác đều \[ABCDEF\] nội tiếp đường tròn \(\left( {O;R} \right)\)
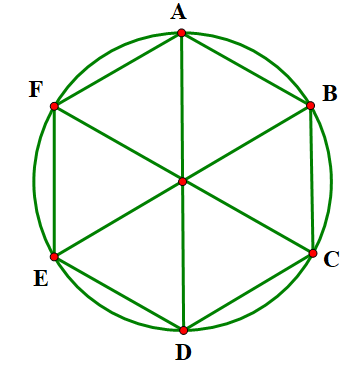
Vì \[ABCDEF\] là lục giác đều \( \Rightarrow AB = BC = CD = DE = EF = FA\)
Xét tam giác\(AOB\)cân tại \(O\) có nên đều \( \Rightarrow AB = R\).
Chứng minh tương tự, ta có \(BC = CD = DE;EF = FA = AB = R\).
Vậy cạnh của hình lục giác đều nội tiếp đường tròn \(\left( {O;R} \right)\) là \(R\).
Ghi nhớ: Bán kính đường tròn ngoại tiếp là R .
- Độ dài cạnh tam giác đều nội tiếp là \(R\sqrt 3 \)
- Độ dài cạnh hình vuông nội tiếp là \(R\sqrt 2 \).
- Độ dài cạnh hình lục giác đều nội tiếp là \(R\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
![Cho ngũ giác đều \[ABCDE\] như hình vẽ. a) Tính tổng các góc trong của tam giác \(ABC,ACD,ADE\), từ đó suy ra tổng các góc trong ngũ giác đều \[ABCED.\] b) Tính số đo góc \(E\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/5-1769708579.png)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Tổng các góc trong của tam giác \(ABC\)bằng 1800. Tương tự với hai tam giác còn lại \(ACD\) và \(ADE\) .
Vậy tổng các góc trong của ba tam giác \[ABC,ACD\;v\`a {\rm{ }}ADE\]là :
\( \Rightarrow \) Tổng các góc trong của ngũ giác đều \[ABCED\] là 5400
b) Vì \[ABCED\]là ngũ giác đều nên tất cả các góc đều bằng nhau nên số đo mỗi góc của ngũ giác đều bằng . Vậy số đo góc \(E\) bằng 1080
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập