2 bài tập Tính toán (có lời giải)

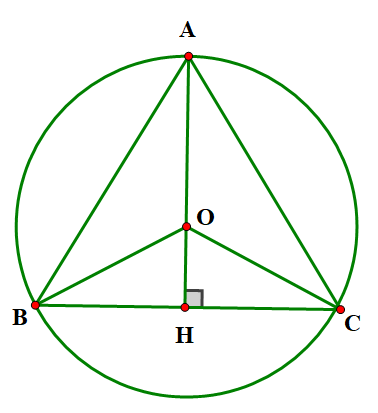
a) • Vẽ tam giác đều \(ABC\) nội tiếp đường tròn \(\left( {O;R} \right)\). Vẽ đường cao \(AH\), ta có:\(AB = AC;OB = OC = R\)

Nên \(A,O,H\) thuộc đường trung trực của \(BC\) vì đều nên \(O\) là trọng tâm của tam giác.

Ta có \(AH = \frac{3}{2}AO = \frac{3}{2}R{\rm{ }}(1)\) (tính chất trọng tâm). Lại có \(AH\) là đường cao của tam giác \(ABC\) đều nên \(AH = \frac{{AB\sqrt 3 }}{2}\). Từ (1) và (2) \( \Rightarrow \frac{3}{2}R = \frac{{AB\sqrt 3 }}{2} \Rightarrow AB = \frac{{3R}}{{\sqrt 3 }} = \sqrt 3 .R\)

Vậy cạnh của tam giác đều nội tiếp đường tròn \(\left( {O;R} \right)\) là \(\sqrt 3 {\rm{.R}}\).

- Vẽ hình vuông\(ABCD\) nội tiếp đường tròn \(\left( {O;R} \right)\).

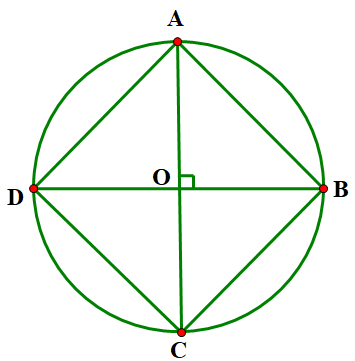
Ta có: \({\rm{AC}} \bot {\rm{BD}}\) (tính chất hai đường chéo hình vuông). Xét tam giác \(AOB\) vuông tại \(O\).

Theo định lí Pythgore, ta có:\(A{B^2} = O{A^2} + O{B^2} = {R^2} + {R^2} = 2{R^2} \Rightarrow AB = \sqrt {2{R^2}} = R\sqrt 2 \)

Vậy cạnh của hình vuông nội tiếp đường tròn \(\left( {O;R} \right)\) là \(R\sqrt 2 \).

- Vẽ lục giác đều \[ABCDEF\] nội tiếp đường tròn \(\left( {O;R} \right)\)

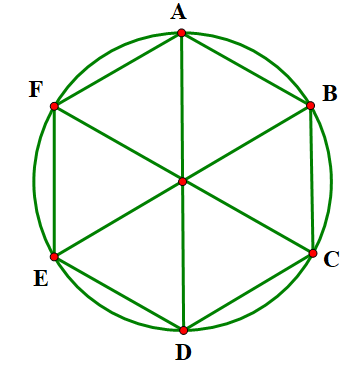
Vì \[ABCDEF\] là lục giác đều \( \Rightarrow AB = BC = CD = DE = EF = FA\)

$\Rightarrow sd\stackrel{⏜}{AB}=sd\stackrel{⏜}{BC}=sd\stackrel{⏜}{CD}=sd\stackrel{⏜}{DE}=sd\stackrel{⏜}{EF}=sd\stackrel{⏜}{FA}$

$\Rightarrow \widehat{AOB}=\widehat{BOC}=\widehat{COD}=\widehat{DOE}=\widehat{EOF}=\widehat{FOA}=\frac{360}{6}={60}^{°}$

Xét tam giác\(AOB\)cân tại \(O\) có $\widehat{\text{AOB}}={60}^{°}$ nên đều \( \Rightarrow AB = R\).

Chứng minh tương tự, ta có \(BC = CD = DE;EF = FA = AB = R\).

Vậy cạnh của hình lục giác đều nội tiếp đường tròn \(\left( {O;R} \right)\) là \(R\).

Ghi nhớ: Bán kính đường tròn ngoại tiếp là R .

- Độ dài cạnh tam giác đều nội tiếp là \(R\sqrt 3 \)

- Độ dài cạnh hình vuông nội tiếp là \(R\sqrt 2 \).

- Độ dài cạnh hình lục giác đều nội tiếp là \(R\).