Chứng minh rằng hàm số \[y = - 5{x^2}\] có các tính chất sau:
a) \[y\] không dương với mọi giá trị của \[x\].
b) nếu \[\left| x \right|\] gấp \[n\] lần thì \[y\] gấp \[{n^2}\] lần.
Chứng minh rằng hàm số \[y = - 5{x^2}\] có các tính chất sau:
a) \[y\] không dương với mọi giá trị của \[x\].
b) nếu \[\left| x \right|\] gấp \[n\] lần thì \[y\] gấp \[{n^2}\] lần.
Quảng cáo
Trả lời:
a) Vì \( - 5{x^2} \le 0,\forall x \in R\)nên \(y \le 0\).
b) Để biểu thị \(\left| x \right|\) gấp n lần cho ta x hai giá trị là K và nK \(\left( {K \ne 0} \right)\).
Các giá trị tương ứng của y là \( - 3{K^2}\)và \( - 3{n^2}{K^2}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a)
- Bảng giá trị của \[y\] tương ứng với giá trị của \[x\] như sau:
|
\[x\] |
\[ - 2\] |
\[ - 1\] |
\[0\] |
\[1\] |
\[2\] |
|
\[y = {x^2}\] |
\[4\] |
\[1\] |
\[0\] |
\[1\] |
\[4\] |
- Vẽ các điểm \[A\left( { - 2;4} \right),B\left( { - 1;1} \right),O\left( {0;0} \right),C\left( {1;1} \right),D\left( {2;4} \right)\] thuộc đồ thị hàm số \(y = {x^2}\) trong mặt phẳng \[Oxy\].
- Vẽ đường parabol đi qua các điểm trên, ta nhận được đồ thị của hàm số \(y = {x^2}\)
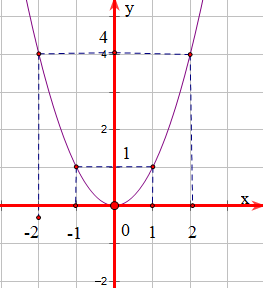
b) Gọi \(C\) là điểm thuộc \(\left( P \right)\) có tung độ bằng 16.
Ta có: \({y_C} = 16 \Leftrightarrow {x^2}_C = 16 \Leftrightarrow {x_C} = \pm 4\). Vậy \(C\left( {4;16} \right)\) hoặc \(C\left( { - 4;16} \right)\).
c) Gọi \(D\) là điểm thuộc \(\left( P \right)\) cách đều hai trục tọa độ.
Ta có: \(d\left( {D,Ox} \right) = \left| {{y_D}} \right| = x_D^2;d\left( {D,Oy} \right) = \left| {{x_D}} \right|\).
Theo giả thiết ta có: \(x_D^2 = \left| {{x_D}} \right| \Leftrightarrow \left| {{x_D}} \right| = 0\) (loại) hoặc \(\left| {{x_D}} \right| = 1\).
Vậy \(D\left( {1;1} \right)\) hoặc \(D\left( { - 1;1} \right)\).
Lời giải
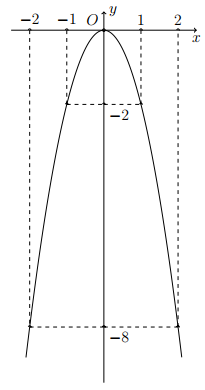
1. \((P)\) đi qua điểm \(A(1; - 2)\) khi và chỉ khi \( - 2 = a{.1^2} \Leftrightarrow a = - 2\).
2. Bảng giá trị

Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.