Trong không gian \(Oxyz\), tìm tất cả các giá trị thực của tham số \(m\) để khoảng cách từ điểm \(I\left( {2; - 1; - 2} \right)\) đến mặt phẳng \(\left( P \right):4x - 3y - m = 0\) bằng 2.
Trong không gian \(Oxyz\), tìm tất cả các giá trị thực của tham số \(m\) để khoảng cách từ điểm \(I\left( {2; - 1; - 2} \right)\) đến mặt phẳng \(\left( P \right):4x - 3y - m = 0\) bằng 2.
A. \(m = 1\).
B. \(m = - 1\) hoặc \(m = - 21\).
Câu hỏi trong đề: Đề kiểm tra Phương trình mặt phẳng (có lời giải) !!
Quảng cáo
Trả lời:
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
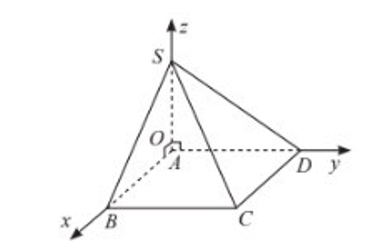
Trục \(Ox\)chứa điểm \(O\left( {0\,;\,0\,;\,0} \right)\) và điểm \(B\left( {1\,;\,0\,;\,0} \right)\).
Do mặt phẳng \(\left( P \right)\) đi qua điểm \(A\left( {1\,;\,2\,;\, - 3} \right)\) và chứa trục \(Ox\) nên mặt phẳng \(\left( P \right)\) có cặp vectơ chỉ phương:
\(\begin{array}{l}\overrightarrow {OA} = \left( {1\,;\,2\,;\, - 3} \right)\\\overrightarrow {OB} = \left( {1\,;\,0\,;\,0} \right)\end{array}\)
Do đó mặt phẳng \(\left( P \right)\) có vectơ pháp tuyến: \(\overrightarrow n = \left[ {\overrightarrow {OA} ;\overrightarrow {OB} } \right] = \left( {0\,;\, - 3\,;\, - 2} \right)\).
Phương trình mặt phẳng là: \(0\left( {x - 0} \right) - 3\left( {y - 0} \right) - 2\left( {z - 0} \right) = 0 \Leftrightarrow 3y + 2z = 0.\)
Vậy \[2a + 3c - d = 6\].Lời giải
Phương trình mặt phẳng \(\left( \alpha \right)\) có dạng: \[ax + by + cz + d = 0\].
Do \[C \in \left( \alpha \right) \Rightarrow 2a + b + d = 0 \Rightarrow d = - 2a - b\quad \left( 1 \right)\].
Do \[D \in \left( \alpha \right) \Rightarrow a + 4b + c + d = 0 \Rightarrow c = - a - 4b - d = - a - 4b + 2a + b = a - 3b\quad \left( 2 \right)\]
Ta có:
\[\begin{array}{l}{d_{\left( {A;\left( \alpha \right)} \right)}} = {d_{\left( {B;\left( \alpha \right)} \right)}}\\\frac{{\left| {1 + c.2 + d} \right|}}{{\sqrt {{1^2} + {b^2} + {c^2}} }} = \frac{{\left| {1 + 2b - 3c + d} \right|}}{{\sqrt {{1^2} + {b^2} + {c^2}} }} \Leftrightarrow \left| {2c + d + 1} \right| = \left| {2b - 3c + d + 1} \right|\\ \Leftrightarrow \left| {2 - 6b - 2 - b + 1} \right| = \left| {2b - 3 + 9b - 2 - b + 1} \right| \Leftrightarrow \left| {1 - 7b} \right| = \left| {10b - 4} \right|\\ \Leftrightarrow \left[ \begin{array}{l}1 - 7b = 10b - 4\\1 - 7b = 4 - 10b\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}b = \frac{{17}}{5}\quad (l)\\b = 1{\kern 1pt} \quad (tm)\end{array} \right..\end{array}\]
Với \[b = 1 \Rightarrow \left\{ \begin{array}{l}c = - 2\\d = - 3\end{array} \right.\].
Phương trình mặt phẳng là: \(\;x + y - 2z - 3 = 0\).
Vậy \[5b + c + d = 5.1 - 2 - 3 = 0\].Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(4x - 5y + z + 24 = 0\).
B. \(x - 2z + 1 = 0\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
a) Một vectơ pháp tuyến của mặt phẳng \(\left( P \right)\) là \(\overrightarrow n \left( {6\,;\,3\,;2} \right)\).
b) Phương trình mặt phẳng \[\left( P \right)\]là \[\frac{x}{1} + \frac{y}{2} + \frac{z}{3} = 0.\].
c) Điểm \[M\left( {3;0; - 2} \right)\]thuộc mặt phẳng \[\left( P \right)\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.