Cho mặt cầu có phương trình \({(x - 2)^2} + {\left( {y + 3} \right)^2} + {(z - 4)^2} = 36\). Điểm\(A\left( {4; - 3;2} \right)\) nằm trong, nằm ngoài hay nằm trên mặt cầu đó?

   Khoảng cách từ tâm đèn đến mặt biển là \(84 + 26 = 110\,m\).

Mặt cầu mô tả ranh giới vùng phủ sáng trên biển của hải đăng có tâm  \(I\left( {12.040.271\,;\,1.418.620\,;\,110} \right)\),  bán kính  \(R = 50000\,\left( m \right)\).

 b) Sai

Phương trình mặt cầu mô tả ranh giới vùng phủ sáng trên biển của hải đăng là

\[\]\(\left( S \right)\)  \[{\left( {x - 12.040.271} \right)^2} + {\left( {y - 1.418.620} \right)^2} + {\left( {z - 110} \right)^2} = {50.000^2}\] .

c) Đúng

Ta có

\[I{B^2} = {\left( {12.026.000 - 12.040.271} \right)^2} + {\left( {1.461.000 - 1.418.620} \right)^2} + {\left( {0 - 110} \right)^2} = 1999.737.941 < {R^2}\]

Nên điểm \(B\) nằm trong mặt cầu \(\left( S \right)\). Vậy người đi biển nhìn thấy ánh đèn của ngọn hải đăng.

d) Sai

Đường thẳng \(\Delta \) đi qua \(C\)và có vectơ chỉ phương là vectơ \(\overrightarrow i  = \left( {1\,;\,0\,;\,0} \right)\) có PTTS là \(\left\{ \begin{array}{l}x = 12.040.452 + t\\y = 1.418.462\\z = 0\end{array} \right.\).

Tìm điểm \(N\) là giao điểm của \(\Delta \) và mặt cầu \(\left( S \right)\):

\[{\left( {12.040.452 + t - 12.040.271} \right)^2} + {\left( {1.418.462 - 1.418.620} \right)^2} + {\left( {0 - 110} \right)^2} = {50.000^2}\]

\[ \Leftrightarrow {\left( {181 + t} \right)^2} = 2.499.962.936 \Rightarrow \left[ \begin{array}{l}t \approx 49.818,6\\t \approx  - 50.180\end{array} \right.\].

Do tàu chuyển động cùng hướng với hướng của vectơ đơn vị \(\overrightarrow i \) nên \(t > 0\)\( \Rightarrow t \approx 49.818,6\)

\( \Rightarrow \)\(N\left( {12.090.270,6\,;\,1.418.620\,;\,0} \right)\) \( \Rightarrow CN \approx 49.818,6\,m\).

Vậy tàu di chuyển tối đa 49.818 m để có thể nhìn thấy đèn của ngọn hải đăng

a) SAI

Các hệ số \(\left\{ \begin{array}{l} - 2a =  - 2\\ - 2b =  - 4\\ - 2c =  - 6\\d =  - 11\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 2\\c = 3\\d =  - 11\end{array} \right.\)

\( \Rightarrow \) Mặt cầu \((S)\) có tâm \(I\left( {1;2;3} \right)\) và bán kính \(R = \sqrt {{a^2} + {b^2} + {c^2} - d}  = 5\).

b) ĐÚNG

Mặt phẳng \(\left( Q \right)\) tiếp xúc với mặt cầu \(\left( S \right)\) tại điểm \(A\left( {1;2;8} \right)\)

\( \Rightarrow \) \(\left( Q \right)\) có vtpt \(\overrightarrow n  = \left( {0;0;5} \right)\) và qua \(A\left( {1;2;8} \right)\)

\( \Rightarrow \) \(\left( Q \right):0.\left( {x - 1} \right) + 0.\left( {y - 2} \right) + 5\left( {z - 8} \right) = 0 \Leftrightarrow \left( Q \right):z = 8\).

c) ĐÚNG

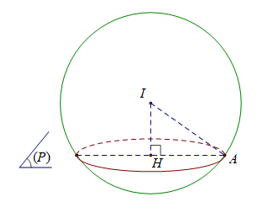
Do \(d\left[ {I,\left( P \right)} \right] = \frac{{\left| {1 + 2 + 3 - 3} \right|}}{{\sqrt {{1^2} + {1^2} + {1^2}} }} = \sqrt 3  < 5 = R\) nên \(\left( P \right)\) cắt mặt cầu \(\left( S \right)\) theo giao tuyến là đường tròn tâm \(H\), bán kính \(HA = \sqrt {{R^2} - {d^2}\left[ {I,(P)} \right]}  = \sqrt {{5^2} - {{\left( {\sqrt 3 } \right)}^2}}  = \sqrt {22} \)

d) SAI

Gọi \(\left( {{x_0},{y_0},{z_0}} \right)\) là một điểm nguyên nằm trên bề mặt của mặt cầu \(\left( S \right)\).

Ta có  \(x_0^2 + y_0^2 + z_0^2 - 2{x_0} - 4{y_0} - 6{z_0} - 11 = 0\)

\( \Leftrightarrow {\left( {{x_0} - 1} \right)^2} + {\left( {{y_0} - 2} \right)^2} + {\left( {{z_0} - 3} \right)^2} = 25\)

Đặt \(\left\{ \begin{array}{l}a = {x_0} - 1\\b = {y_0} - 2\\c = {z_0} - 3\end{array} \right.\) thì  \({a^2} + {b^2} + {c^2} = 25\) (*)  và \(a,b,c \in \mathbb{Z}\).

Số bộ \(\left( {a;b;c} \right)\) bằng với số bộ \(\left( {x;y;z} \right)\).

Do \({a^2},\,{b^2},{c^2}\) vai trò như nhau nên có thể giả sử \({a^2} \le {b^2} \le {c^2}\).

\({a^2} + {b^2} + {c^2} = 25 \Rightarrow 3{a^2} \le 25 \Rightarrow {a^2} \in \left\{ {0;1;4} \right\}\).

Với \({a^2} = 4\),

\(\left( * \right) \Rightarrow \) \({b^2} + {c^2} = 21\) à không có \(b,c\) nguyên.

 Với \({a^2} = 1\),

\(\left( * \right) \Rightarrow \) \({b^2} + {c^2} = 24 \Rightarrow \) không tồn tại \(b,c\) nguyên.

Với \({a^2} = 0\),

 \(\left( * \right) \Rightarrow \) \({b^2} + {c^2} = 25 = {3^2} + {4^2}\)

Chọn vị trí cho số \(0\)trong bộ \(\left( {a;b;c} \right)\) có \(3\)cách.

Chọn \(3\) hoặc \( - 3\) và xếp vào một vị trí trong bộ \(\left( {a;b;c} \right)\) có \(2.2 = 4\)cách.

Vị trí còn lại cho \(4\) hoặc \( - 4\) trong bộ \(\left( {a;b;c} \right)\) có \(2\)cách.

Vậy có \(3.4.2 = 24\) bộ \(\left( {a;b;c} \right)\).

Vậy có \(24\) bộ \(\left( {a;b;c} \right)\) hay \(24\) điểm nguyên nằm trên mặt cầu \(\left( S \right)\).