Trong vật lí, sự phân rã các chất phóng xạ được cho bởi công thức:

\(m(t) = {m_0}{\left( {\frac{1}{2}} \right)^{\frac{t}{T}}}\)Trong đó, \({m_0}\) là khối lượng chất phóng xạ ban đầu (tại thời điểm \(\left. {t = 0} \right),m(t)\) là khối lượng chất phóng xạ tại thời điểm \(t\) và \(T\) là chu kì bán rã.

Hạt nhân Poloni \((Po)\) là chất phóng xạ \(\alpha \) có chu kì bán rã 138 ngày. Giả sử lúc đầu có 100 Poloni. Tính khối lượng Poloni còn lại sau 100 ngày theo đơn vị gam (làm tròn kết quả đến phần nghìn).

Đầu tiên ta tính giá trị của ngôi nhà sau \(12\) năm:

Giá trị ngôi nhà sau 2 năm: \({10^9} + {10^9}.0,05 = {10^9}.\left( {1 + 0,05} \right)\)

Giá trị ngôi nhà sau 4 năm: \({10^9} + {10^9}.0,05 + \left( {{{10}^9} + {{10}^9}.0,05} \right).0,05 = {10^9}.{\left( {1 + 0,05} \right)^2}\)

Lần lượt ta có giá trị ngôi nhà sau 12 năm: \({10^9} + {10^9}.0,05 + \left( {{{10}^9} + {{10}^9}.0,05} \right).0,05 = {10^9}.{\left( {1 + 0,05} \right)^6}\)

Sau khi chi tiêu hàng tháng thì số tiền tiết kiệm là \(40\% \) lương.

Có nghĩa là trong hai năm \(2023 - 2024\), số tiền tiết kiệm là: \(24.0,4a\)

Trong hai năm tiếp theo \(2025 - 2026\), số tiền tiết kiệm là: \(24.0,4a\left( {1 + 0,01} \right)\)

Tương tự vậy số tiền tiết kiệm được trong 12 năm là: \(24.0,4a\left[ {1 + \left( {1 + 0,1} \right) + {{\left( {1 + 0,1} \right)}^2} + {{\left( {1 + 0,1} \right)}^3} + {{\left( {1 + 0,1} \right)}^4} + {{\left( {1 + 0,1} \right)}^5}} \right] = 74,069856a\)

Để mua được nhà thì số tiền trên phải bằng số tiền sau \(12\) năm: \(74,069856a = {10^9}.1,{05^6} \Rightarrow a = 18092321\)

Vậy số \(a\) gần bằng \(18092000\).

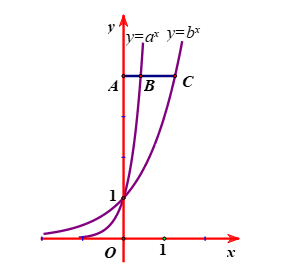
Theo đề bài ta có tọa độ các điểm là \(A\left( {0;4} \right)\,,\,B\left( {{{\log }_a}4;4} \right)\) và \(C\left( {{{\log }_b}4;4} \right)\).

Theo giả thiết \(AC = 3AB \Leftrightarrow {\log _b}4 = 3{\log _a}4\)\( \Leftrightarrow \frac{1}{{{{\log }_4}b}} = \frac{3}{{{{\log }_4}a}}\)