Câu hỏi:
13/07/2024 478Câu hỏi trong đề: Giải Sách Bài Tập Toán 8 Tập 1 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Vẽ được duy nhât một hình thm có 2 đường chéo là a và 1/2 a
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
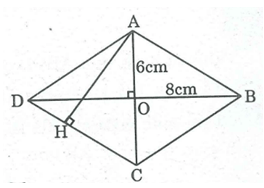
ABCD là hình thoi có O là giao điểm của hai đường chéo nên:
AO = OC = 6cm; OB = OD = 8cm
Trong tam giác vuông OAB, ta có:
= 100
AB = 10 (cm)
Kẻ AH ⊥ CD (H ∈ CD)
Ta có: = AH.CD ⇒ AH = / CD = 96/10 = 9,6 (cm)
Lời giải
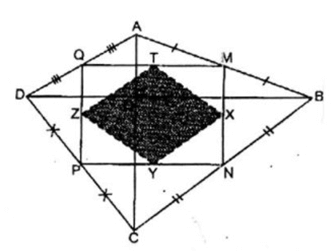
Trong ABD ta có:
M là trung điểm của AB
Q là trung điểm của AD nên MQ là đường trung bình của ABD.
⇒ MQ // BD và MQ = 1/2 BD (tính chất đường trung bình của tam giác) (1)
Trong CBD ta có:
N là trung điểm của BC
P là trung điểm của CD
nên NP là đường trung bình của CBD
⇒ NP // BD và NP = 1/2 BD (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: MQ // NP và MQ = NP nên tứ giác MNPQ là hình bình hành
AC ⊥ BD (gt)
MQ // BD
Suy ra: AC ⊥ MQ
Trong ABC có MN là đường trung bình ⇒ MN // AC
Suy ra: MN ⊥ MQ hay (NMQ) =
Vậy tứ giác MNPQ là hình chữ nhật.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo