Phòng luyện đề thi giữa kì 1 năm học 2026-2027 tất cả các môn lớp 1-12

✕

Giảm 50% Kích hoạt VIP

Kích hoạt VIP

Tạo VIP

Câu hỏi:

18/06/2020 1,978

Tính thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox hình phẳng giới hạn bởi các đường 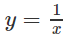, y = 0, x = 1 và x = a (a > 1). Gọi thể tích đó là V(a). Xác định thể tích của vật thể khi a → + $\infty$ (tức là ).

Xem lời giải

Câu hỏi trong đề: Giải sbt Giải tích 12 Bài 3: Ứng dụng của tích phân trong hình học !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Giải sách bài tập Toán 12 | Giải sbt Toán 12

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tính diện tích hình phẳng giới hạn bởi các đường sau:
a) y = 2x – $x^{2}$ , x + y = 2 ;
b) y = $x^{3}$ – 12x, y = $x^{2}$
c) x + y = 1, x + y = -1, x – y = 1, x – y = -1;
d)
e) y = $x^{3}$ – 1 và tiếp tuyến với y = $x^{3}$ – 1 tại điểm (-1; -2).

Xem đáp án

Lời giải

a) Đáp số: 1/6

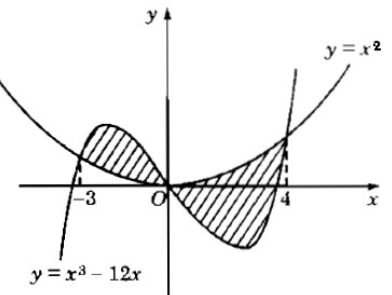
b) Đáp số: 937/12.

Hướng dẫn:

Giải sách bài tập Toán 12 | Giải sbt Toán 12

c) Đáp số: 2

Hướng dẫn: Giải sách bài tập Toán 12 | Giải sbt Toán 12

d) π/2 - 1

Hướng dẫn:

Giải sách bài tập Toán 12 | Giải sbt Toán 12

Đặt x = tan t để tính Giải sách bài tập Toán 12 | Giải sbt Toán 12

e) Đáp số: 27/4

Hướng dẫn: Phương trình tiếp tuyến tại (-1; -2) là y = 3x + 1. Do đó, diện tích :

Giải sách bài tập Toán 12 | Giải sbt Toán 12

Câu 2

Cho hình phẳng H giới hạn bởi các đường: y = f(x), y = 0, x = b và x = a (trong đó hàm số f(x) liên tục trên đoạn [b,a]). Thể tích khối tròn xoay tạo nên bởi phép quay H quanh trục Ox được cho bởi công thức:

Xem đáp án

Lời giải

Đáp án: C.

Lưu ý ở đây b là cận dưới còn a là cận trên (b ≤ a), vậy A sai, B thiếu hệ số π, D có hệ số $π^{2}$ .

Câu 3

Tính thể tích vật thể:
a) Có đáy là một tam giác cho bởi: y = x , y = 0 , và x = 1. Mỗi thiết diện vuông góc với trục Ox là một hình vuông.
b) Có đáy là một hình tròn giới hạn bởi $x^{2}$ + $y^{2}$ = 1. Mỗi thiết diện vuông góc với trục Ox là một hình vuông.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Tính thể tích các khối tròn xoay khi quay hình phẳng xác định bởi:
a) y = 2 – $x^{2}$ , y = 1 , quanh trục Ox.
b) y = 2x – $x^{2}$ , y = x , quanh trục Ox.
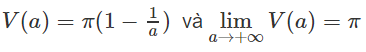
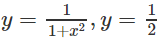
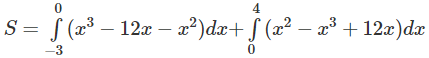
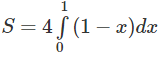
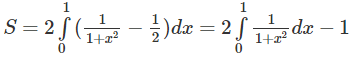
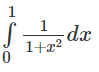
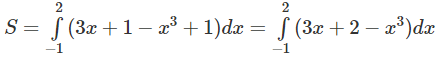
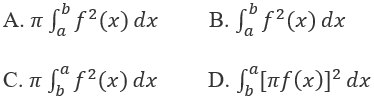
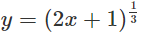c) ,x = 0, y = 3, quanh trục Oy.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Một hình phẳng được giới hạn bởi y = $e^{- x}$ , y = 0, x = 0, x = 1. Ta chia đoạn [0; 1] thành n phần bằng nhau tạo thành một hình bậc thang (bởi n hình chữ nhật con như Hình bên).
a) Tính diện tích Sn của hình bậc thang (tổng diện tích của n hình chữ nhật con).
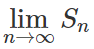b) Tìm và so sánh với cách tính diện tích hình phẳng này bằng công thức tích phân.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Diện tích hình phẳng P giới hạn bởi các đường: $y_{1}$ = x, $y_{2}$ = 2x, $y_{3}$ = 2 - x bằng:
A. 1 B. 2/3
C. 2 D. 1/3

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Khóa học 1 - 12

THPT

THCS

Phòng luyện đề

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ô Ôn vào 10

Ôn vào 6

Ô Ôn vào 6

Tài liệu

THPT

THCS

Tin Tuyển Sinh