Hàm số nào sau đây không đồng biến trên khoảng (-∞;+∞) A. y=x-1x+2 B. y=x3+2 C. y = x + 1 D. y=x5+x3-1

Câu hỏi:

10/07/2020 610

Hàm số nào sau đây không đồng biến trên khoảng (-∞;+∞)

A. $y = \frac{x - 1}{x + 2}$

B. $y = x^{3} + 2$

C. y = x + 1

D. $y = x^{5} + x^{3} - 1$

Xem lời giải

Câu hỏi trong đề: Top 4 Đề thi Toán lớp 12 Học kì 1 chọn lọc, có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án A

Phương pháp:

* Phương pháp xét sự đồng biến, nghịch biến của các hàm số:

- Bước 1: Tìm tập xác định, tính f'(x)

- Bước 2: Tìm các điểm tại đó f'(x) = 0 hoặc f'(x) không xác định

- Bước 3: Sắp xếp các điểm đó theo thứ tự tăng dần và lập bảng biến thiên

- Bước 4: Kết luận về các khoảng đồng biến, nghịch biến của hàm số.

Cách giải:

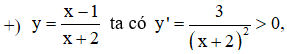
=> Hàm số đồng biến trên các khoảng (-∞;-2);(-2;+∞)

+) y = x3 + 2 ⇒ y'= 3x2 ≥ 0,∀ x∈R: Hàm số đồng biến trên R.

+) y = x + 1 ⇒ y' = 1 > 0, ∀ x∈R: Hàm số đồng biến trên R.

+) y = x5 + x3 - 1 ⇒ y' = 5x4 + 3x2 ≥ 0, ∀ x ∈ R; y' = 0 ⇔ x = 0 ⇒ Hàm số đồng biến trên R.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Đạo hàm của hàm số y = xln⁡x trên khoảng (0;+∞) là

A. y' = ln x

B. y' = 1

C. $y' = \frac{1}{x}$

D. y' = 1 + ln x

Lời giải

Đáp án D

Phương pháp: (uv)' = u'v + uv'

Cách giải:

Câu 2

Ông An gửi 100 triệu đồng vào ngân hàng với hình thức lãi kép, kỳ hạn 1 năm với lãi suất 8%/năm. Sau 5 năm ông rút toàn bộ tiền và dùng một nửa để sửa nhà, số tiền còn lại ông tiếp tục gửi vào ngân hàng với kỳ hạn và lãi suất như lần trước. Số tiền lãi mà ông An nhận được sau 10 năm gửi gần nhất với giá trị nào sau đây?

A. 34,480 triệu.

B. 81,413 triệu.

C. 107,946 triệu.

D. 46,933 triệu.

Lời giải

Đáp án A

Phương pháp:

Công thức lãi kép, không kỳ hạn: An = M(1 + r%)n

Với:

An là số tiền nhận được sau tháng thứ n,

M là số tiền gửi ban đầu,

n là thời gian gửi tiền (tháng),

r là lãi suất định kì (%)

Cách giải:

Số tiền ông An rút lần 1 là: 100.(1 + 8%)5 = 146,9328077 (triệu đồng)

Số tiền ông An gửi lần 2 là: 146.9328077 : 2 = 73,46640384 (triệu đồng)

Số tiền ông An rút lần 2 (gửi 5 năm tiếp theo) là:

73,46640384.(1 + 8%)5 = 107,9462499 (triệu đồng)

Số tiền lãi là: 107,9462499 - 73,4660384 = 34,47984602 ≈ 34,480 (triệu đồng).

Câu 3

Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?

A. $y = x^{3} - 3 x^{2} + 2$

B. $y = x^{3} + 3 x^{2} + 2$

C. $y = - x^{3} + 3 x^{2} + 2$

D. $y = - x^{3} + 6 x^{2} + 2$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Một xưởng in có 8 máy in, mỗi máy in được 4000 bản in khổ giấy A4 trong một giờ. Chi phí để bảo trì, vận hành một máy mỗi lần in là 50 nghìn đồng. Chi phí in ấn của n máy chạy trong một giờ là 20(3n + 5) nghìn đồng. Hỏi nếu in 50 000 bản in khổ A4 thì phải sử dụng bao nhiêu máy để thu được lãi nhiều nhất?

A. 6 máy

B. 7 máy

C. 5 máy

D. 4 máy

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Nguyên hàm của f(x) = xcos⁡x làa

A. $F (x) = - x \sin x - \cos x + C$

B. $F (x) = x \sin x + \cos x + C$

C. $F (x) = x \sin x - \cos x + C$

D. $F (x) = - x \sin x + \cos x + C$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Tìm mệnh đề đúng trong các mệnh đề sau

A. Đồ thị các hàm số $y = a^{x}$ và $y = {(\frac{1}{a})}^{x} 0 < a \neq 1$ đối xứng nhau qua trục tung.

B. Hàm số $y = a^{x}$ , 0 < a ≠ 1 đồng biến trên R

C. Hàm số $y = a^{x}$ , a > 1 nghịch biến trên R

D. Đồ thị hàm số $y = a^{x}$ , 0 < a ≠ 1 luôn đi qua điểm có tọa độ (a;1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho hàm số $f (x) = \frac{1}{2 x + 3}$ . Gọi F(x) là một nguyên hàm của f(x). Khẳng định nào sau là sai?

A. $F (x) = \frac{\ln |2 x + 3|}{2} + 1$

B. $F (x) = \frac{\ln {|2 x + 3|}^{2}}{4} + 3$

C. $F (x) = \frac{\ln |4 x + 6|}{4} + 3$

D. $F (x) = \frac{\ln |x + \frac{3}{2}|}{2} + 4$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Hàm số nào sau đây không đồng biến trên khoảng (-∞;+∞)

Đạo hàm của hàm số y = xln⁡x trên khoảng (0;+∞) là

Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?

Nguyên hàm của f(x) = xcos⁡x làa

Tìm mệnh đề đúng trong các mệnh đề sau

Cho hàm số fx=12x+3. Gọi F(x) là một nguyên hàm của f(x). Khẳng định nào sau là sai?

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho hàm số $f (x) = \frac{1}{2 x + 3}$ . Gọi F(x) là một nguyên hàm của f(x). Khẳng định nào sau là sai?