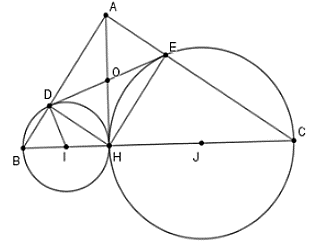
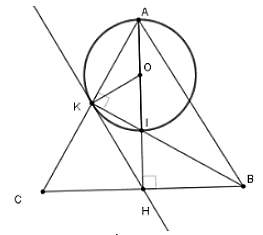
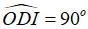Cho tam giác vuông ABC tại A, đường cao AH. Đường tròn đường kính BH cắt AB tại D, đường tròn đường kính CH cắt AC tại E. Chọn khẳng định sai trong các khẳng định sau
A. DE là cát tuyến của đường tròn đường kính BH
B. DE là tiếp tuyến của đường tròn đường kính BH
C. Tứ giác AEHD là hình chữ nhật
D. DE ⊥ DI (với I là trung điểm BH)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án A
Gọi I, J lần lượt là trung điểm của BH và CH.
Để chứng minh DE là tiếp tuyến của đường tròn tâm I đường kính BH ta chứng minh ID ⊥ DE hay 
Vì D, E lần lượt thuộc đường tròn đường kính BH và HC
Nên DE là tiếp tuyến của đường tròn đường kính BH
Từ chứng minh trên suy ra các phương án B, C, D đúng
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án A
+) Gọi O là trung điểm AI. Xét tam giác vuông AIK có
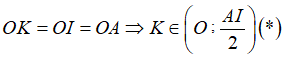
+) Xét tam giác OKA cân tại O (vì OA=OK=R) có:
(1)
+) Xét tam giác CKB vuông tại K (vì ) có:
H là trung điểm CB (vì tam giác ABC cân tại A có AH là đường cao nên đồng thời là đường trung tuyến)
KH là trung tuyến ứng với cạnh huyền BC
Từ (1) và (2) suy ra (vì )
Mà (**)
Từ (*) và (**) suy ra HK là tiếp tuyến của (O)
Câu 2
A. AC là tiếp tuyến của (B; BA).
B. AB là tiếp tuyến của (A; AC).
C. BC là tiếp tuyến của (A; AC).
D. BC là tiếp tuyến của (A; AB).
Lời giải
Đáp án A
Tam giác ABC có: nên tam giác BAC vuông tại A.
Ta có: AB ⊥ AC tại A và A thuộc đường tròn (B; BA).
Suy ra: AC là tiếp tuyến của (B; BA).
Câu 3
A. AB là tiếp tuyến của (O).
B. BC là tiếp tuyến của (O).
C.CD là tiếp tuyến của (O)
D. Tất cả sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. MB là tiếp tuyến của đường tròn (O; R).
B. Tam giác MAB là tam giác đều.
C. Diện tích tam giác AOM là:
D. MA =
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. AB, BC, CD và DA là các tiếp tuyến của đường tròn (O).
B. AB, BC, CD và DA đều không là tiếp tuyến của đường tròn (O).
C. AC và BD là tiếp tuyến của (O).
D. Tất cả sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. BC là tiếp tuyến của (O).
B. Khoảng cách từ O đến AB là 3 cm.
C. OC = 25/3 cm
D. A hoặc B sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo