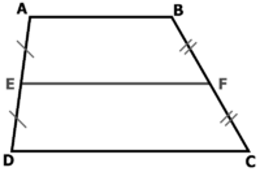
Cho hình thang ABCD có E là trung điểm của AD, F là trung điểm của BC và AB = 4( cm ) và CD = 7( cm ). Tính độ dài đoạn EF.

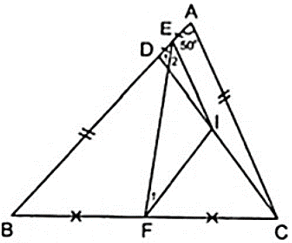
Do E,F lần lượt là trung điểm của cạnh AD,BC theo giả thiết nên ta vẽ thêm I là trung điểm của CD nên EI, FI theo thứ tự lần lượt là đường trung bình của tam giác ACD và BCD.

Đặt BD = AC = 2a

Áp dụng định lý đường trung bình của hai tam giác trên ta có:

( 1 )      FI//BD       ( 2 )       FI = a

( 3 )      EI = a       ( 4 )      EI//AC

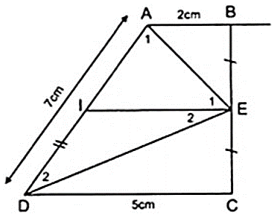
Ta có EI là đường trung bình của hình thang ABCD.

Áp dụng định lý đường trung bình của hình thang ABCD ta có:

IE = (AB + CD)/2 = (2 + 5)/2 = 3,5( cm )       ( 2 )

Từ ( 1 ) và ( 2 ) ta có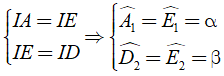 (vì trong tam giác, đối diện với hai cạn bằng nhau là hai góc bằng nhau)

+ Xét tam giác ADE có