Câu hỏi:

19/08/2022 4,888

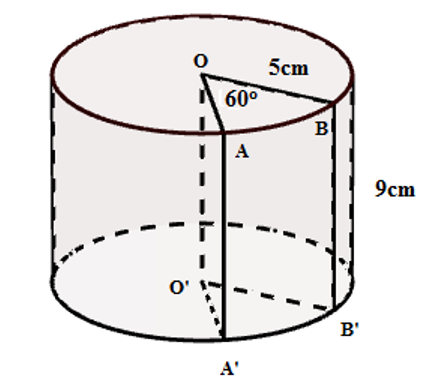
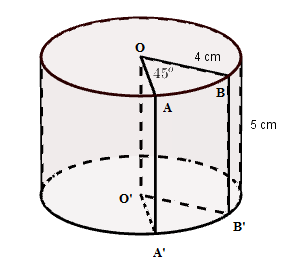
Một hình trụ có thể tích V không đổi. Hỏi bán kính đáy bằng bao nhiêu để diện tích toàn phần của hình trụ đó là nhỏ nhất?

A. $R = \sqrt[3]{\frac{V}{2 π}}$ .

B. $R = \sqrt{\frac{V}{2 π}}$ .

C. $R = \frac{\sqrt[3]{V}}{2 π}$ .

D. $R = 3 \sqrt[3]{\frac{V}{2 π}}$ .

Câu hỏi trong đề: 7 câu Trắc nghiệm Toán 9 Bài 1: Hình trụ. Diện tích xung quanh và thể tích của hình trụ có đáp án (Vận dụng) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án cần chọn là: A

Gọi bán kính đáy và chiều cao của hình trụ lần lượt là R, h (R > 0; h > 0)

Ta có $V = {πR}^{2} h \Rightarrow h = \frac{π}{{πR}^{2}}$ .

Diện tích toàn phần của hình trụ

$S_{t p} = 2 πRh + 2 {πR}^{2} = 2 πR \frac{V}{{πR}^{2}} + 2 {πR}^{2} = \frac{2 V}{R} + 2 {πR}^{2}$

$= \frac{V}{R} + \frac{V}{R} + 2 {πR}^{2} \geq 3 \sqrt[3]{\frac{V}{R} . \frac{V}{R} . 2 {πR}^{2}} = 3 \sqrt[3]{2 {πV}^{2}}$

Dấu “=” xảy ra $\Leftrightarrow \frac{V}{R} = 2 {πR}^{2} \Rightarrow R = \sqrt[3]{\frac{V}{2 π}}$

Vậy với $R = \sqrt[3]{\frac{V}{2 π}}$ thì S_tp đạt giá trị nhỏ nhất là $3 \sqrt[3]{2 {πV}^{2}}$ .

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một trục lăn có dạng hình trụ nằm ngang (như hình vẽ), hình trụ có diện tích một đáy $S = 36 π {cm}^{2}$ và chiều cao h = 8cm. Nếu trục lăn đủ 10 vòng thì diện tích tạo trên sân phẳng là bao nhiêu?

A. $1200 π ({cm}^{2})$ .

B. $480 π ({cm}^{2})$ .

C. $960 π ({cm}^{2})$ .

D. $960 (c m^{2})$ .

Lời giải

Đáp án cần chọn là: C

Bán kính R của đường tròn đáy là ${πR}^{2} = 36 π \Rightarrow R = 6 cm$ .

Diện tích xung quanh của hình trụ $S_{x q} = 2 πRh = 2 π . 6.8 = 96 π ({cm}^{2})$

Vì trục lăn 12 vòng nên diện tích tạo trên sân phẳng là 10.96 = 960 (cm²)

Câu 2

Một trục lăn có dạng hình trụ nằm ngang (như hình vẽ), hình trụ có diện tích một đáy $S = 25 π {cm}^{2}$ và chiều cao h = 10cm. Nếu trục lăn đủ 12 vòng thì diện tích tạo trên sân phẳng là bao nhiêu?

A. $1200 π ({cm}^{2})$ .

B. $600 π ({cm}^{2})$ .

C. $1000 π ({cm}^{2})$ .

D. $1210 π ({cm}^{2})$ .

Lời giải

Đáp án cần chọn là: A

Bán kính R của đường tròn đáy là ${πR}^{2} = 25 π \Rightarrow R = 5 cm$ .

Diện tích xung quanh của hình trụ $S_{x q} = 2 πRh = 2 π . 5.10 = 100 π ({cm}^{2})$ .

Vì trục lăn 12 vòng nên diện tích tạo trên sân phẳng là $12.100 = 1200 (c m^{2})$ .

Câu 3

Cho hình trụ bị cắt bỏ một phần OABB’A’O’ như hình vẽ. Thể tích phần còn lại là:

A. $187, 5 π ({cm}^{3})$ .

B. $187 π ({cm}^{3})$ .

C. $375 π ({cm}^{3})$ .

D. $75 π ({cm}^{3})$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho tam giác ABC (AB < AC) nội tiếp đường tròn (O; R) đường kính BC. Vẽ đường cao AH của tam giác ABC. Đường tròn tâm K đường kính AH cắt AB, AC lần lượt tại D và E. Biết BC = 25cm và AH = 12cm. Hãy tính diện tích xung quanh của hình tạo thành bởi khi cho tứ giác ADHE quay quanh AD.

A. $\frac{3456}{5} π ({cm}^{2})$ .

B. $\frac{3456}{25} π ({cm}^{2})$ .

C. $\frac{1728}{25} π ({cm}^{2})$ .

D. $\frac{7128}{25} π ({cm}^{2})$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Một hình trụ có thể tích 8 $c m^{3}$ không đổi. Hỏi bán kính đáy bằng bao nhiêu để diện tích toàn phần của hình trụ đó là nhỏ nhất?

A. $R = \sqrt{\frac{4}{π}}$ .

B. $R = \sqrt[3]{\frac{4}{π}}$ .

C. $R = \sqrt[3]{4 π}$ .

D. $R = \sqrt[3]{\frac{4}{π}}$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hình trụ bị cắt bỏ một phần OABB’A’O’ như hình vẽ. Thể tích phần còn lại là:

A. $70 π ({cm}^{3})$ .

B. $80 π ({cm}^{3})$ .

C. $60 π ({cm}^{3})$ .

D. $10 π ({cm}^{3})$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Giáo dục công dân

Tin học

Tiếng Anh

Giáo dục Kinh tế và Pháp luật

ĐHQG Hồ Chí Minh

ĐH Bách Khoa

ĐHQG Hà Nội

Bộ Công an

ĐHSP Hà Nội

Bằng lái xe

English Test

IT Test

Đại học

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Tin học

Giáo dục Kinh tế và Pháp luật

Global success

iLearn Smart World

Friends Global

Explore new worlds

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học