Câu hỏi:
11/07/2024 1,399(3 điểm):
Cho tam giác ABC, các điểm M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC. Trên tia đối của tia NP lấy điểm D sao cho ND = NP.a) Chứng minh: Tứ giác ADCP là hình bình hành.
b) Gọi F là giao điểm của MN và DC. Giả sử MN = 3cm. Tính BC và chứng minh FD = FC.
c) Gọi H là giao điểm của AP và MN; I là giao điểm của NP và HC. Chứng minh: B, I, F thẳng hàng.
Câu hỏi trong đề: Đề thi Giữa kì 1 Toán 8 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
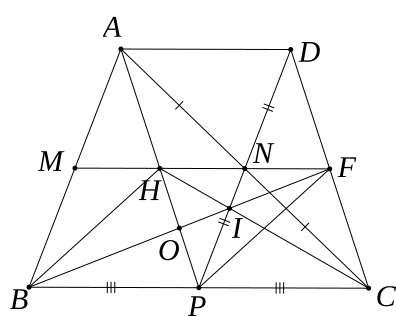
a) Xét tứ giác ADCP có:
N là trung điểm của AC
N là trung điểm của DP (ND = NP)
⇒ tứ giác ADCP là hình bình hành.
b) Xét tam giác ABC có:
M là trung điểm AB
N là trung điểm AC
⇒ MN là đường trung bình tam giác ABC
⇒ MN//BC, \(MN = \frac{1}{2}BC\)
⇒ BC = 2MN = 2.3 = 6cm
Ta có MN//BC (MN là đường trung bình tam giác ABC)
⇒ NF//PC
Trong tam giác DCP có:
N là trung điểm của DP
NF//PC
⇒ F là trung điểm của DC
Hay DF = FC
Suy ra NF là đường trung bình của ΔDCP.
\( \Rightarrow NF = \frac{1}{2}PC\)
c) Chứng minh tương tự: HN là đường trung bình của ΔACP và H là trung điểm của AP
\( \Rightarrow HN = \frac{1}{2}PC\)
Ta có: \(HF = HN + NF = \frac{1}{2}PC + \frac{1}{2}PC = PC\)
Mà có: PC = PB nên HN= PB
Xét tứ giác BHFP có HN = PB và HN // PB (vì MN//BC)
⇒ BHFP là hình hình hành
Gọi BF cắt HP tại O. Khi đó O là trung điểm của BF và HP.
Trong tam giác APC có CH và PN là đường trung tuyến
và CH cắt PN tại I
I là trọng tâm tam giác APC
\( \Rightarrow PI = \frac{2}{3}PN\)
Trong tam giác PHF có: PN là đường trung tuyến và \(PI = \frac{2}{3}PN\)
I là trọng tâm tam giác PHF
mà có FO là đường trung tuyến (vì O là trung điểm của HP)
I thuộc FO
F, I, O thẳng hàng
mà F, O, B thẳng hàng
nên B, I, F thẳng hàng.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
A = x2+ 5y2– 4xy – 2y + 2x + 2010
= x2+ 4y2+ y2– 4xy – 4y + 2y + 2x + 1 + 1 + 2008
= (x2– 4xy + 4y2) + (2x – 4y) + (y2+ 2y + 1) + 1 + 2008
= (x – 2y)2+ 2(x – 2y) + 1 + (y + 1)2+ 2008
= (x – 2y + 1)2+ (y + 1)2+ 2008
Vì \[{\left( {x--2y + 1} \right)^2} + {\left( {y + 1} \right)^2}\; \ge 0{\rm{ }}\forall x;y\]
Do đó (x – 2y + 1)2+ (y + 1)2+ 2008 ≥ 2008 với mọi x, y
Dấu “=” xảy ra khi x – 2y + 1 = 0 và y + 1 = 0
Ta có:
y + 1 = 0 ⇒ y = – 1
Thay y = – 1 vào x – 2y + 1 = 0
⇒ x – 2.(– 1) + 1 = 0
⇒ x = – 3
Vậy GTNN của A là 2008 khi x = – 3 và y = – 1.
Lời giải
Đáp án đúng là: C
Ta có: 5x2– 10x = 5x(x – 2).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
10 Bài tập Nhận biết đơn thức, đơn thức thu gọn, hệ số, phần biến và bậc của đơn thức (có lời giải)
-
Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án (Đề 5)
-
Dạng 8: Bài luyện tập 3 dạng 4. Tổng hợp có đáp án
-
Dạng 2: Bài luyện tập 1 Dạng 2: Rút gọn phân thức có đáp án
Nhắn tin Zalo