Người ta cắt đôi đoạn dây thép dài 10m thành hai phần. Phần 1 lại cắt thành 6 phần bằng nhau và ghép thành một hình tứ diện, phần 2 lại cắt thành 12 phần bằng nhau và ghép thành một hình lập phương sao cho tổng diện tích xung quanh của hai hình là nhỏ nhất.
Gọi a là độ dài cạnh của hình tứ diện, b là độ dài cạnh của hình lập phương thì a + b là:
Câu hỏi trong đề: Bài tập Hình học không gian cơ bản, nâng cao có lời giải !!
Quảng cáo
Trả lời:
Đáp án C.
Gọi x là chiều dài đoạn thép thứ nhất, 0 < x < 10
=> Cạnh hình tứ diện là (tứ diện là đều)
Cạnh hình lập phương là
Diện tích xung quanh của tứ diện là ![]()
Diện tích xung quanh của lập phương là ![]()
Tổng đạt giá trị nhỏ nhất khi 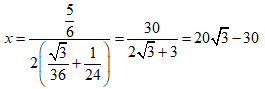
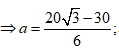
![]()
![]()
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. (AHC')
B. (AA'H)
C. (HAB)
D. (HA'C')
Lời giải
Đáp án A
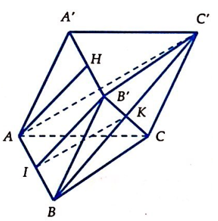
Gọi ![]() và I là trung điểm của AB
và I là trung điểm của AB
Do HB' = AI, HB'//AI => AHB'I là hình bình hành => AH//B'I
Mặt khác KI//AC' nên (AHC')//(B'CI)=> B'C//(AHC')
Lời giải
Đáp án B.

Gọi H là trung điểm AB, G là trọng tâm
Trong mặt phẳng (ABCD), ![]()
Ta có: ![]()
Gọi I là hình chiếu của H lên BD, K là hình chiếu của H lên GI
![]()
Ta có: 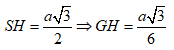
![]()
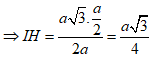
![]()
![]()
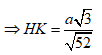
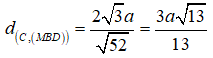

Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.