Có bao nhiêu cặp số nguyên dương\(\left( {x;y} \right)\)thỏa mãn:\(2y{.2^x} = {\log _2}\left( {1 + \frac{{2x}}{y}} \right) + 2y + 3x\)
A. 1.
B. 2.
C. 10.
D. 4.
Câu hỏi trong đề: Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!
Quảng cáo
Trả lời:
Ta có: \(2y{.2^x} = {\log _2}\left( {1 + \frac{{2x}}{y}} \right) + 2y + 3x\)
\(\begin{array}{l} \Leftrightarrow 2y{.2^x} = {\log _2}\left( {y + 2x} \right) - {\log _2}y + 2y + 3x\\ \Leftrightarrow y{.2^{x + 1}} + {\log _2}y + \left( {x + 1} \right) = 1 + {\log _2}\left( {y + 2x} \right) + 2y + 4x\\ \Leftrightarrow y{.2^{x + 1}} + {\log _2}\left( {y{{.2}^{x + 1}}} \right) = {\log _2}\left( {2y + 4x} \right) + \left( {2y + 4x} \right)\,\,\,\,\,\,\,(1)\end{array}\)
Ta thấy \(f\left( t \right) = {\log _2}t + t\) đồng biến trên \((0; + \infty )\) nên
\(\left( 1 \right) \Leftrightarrow y{.2^{x + 1}} = 2y + 4x \Leftrightarrow y{.2^x} = y + 2x \Rightarrow {2^x} = 1 + \frac{{2x}}{y}\) (2)
Do ynguyên dương nên \(1 + \frac{{2x}}{y} \le 1 + 2x\) (3)
Từ (2) và (3) ta có: \({2^x} \le 1 + 2x\) (4)
Xét \(f\left( x \right) = {2^x} - 2x - 1,\,\,x >0\)
\(f'\left( x \right) = {2^x}\ln 2 - 2 >0\,\,,\forall x \ge 3\)\( \Rightarrow f\left( x \right) \ge f\left( 3 \right) = {2^3} - 2.3 - 1 >0\,\,\forall x \ge 3\)
Suy ra \({2^x} - 2x - 1 >0\,\,\forall x \ge 3\)
Từ (4) và do x nguyên dương nên từ\({2^x} \le 1 + 2x \Rightarrow x \in \left\{ {1;2} \right\}\)
Thay \(x = 1\) vào (2) ta có \(y = 2\).
Thay \(x = 2\) vào (2) ta có \(y = \frac{4}{3}\)
Vậy có một cặp số nguyên dương \(\left( {x;y} \right)\)thỏa đề là: \(\left( {1;2} \right)\).
Nhận xét:
Kiên thức sử dụng:
1. Hàm sử dụng hàm đặc trưng để suy ra biểu thức quan hệ giữa x, y đơn giản hơn.
2. Sử dụng đánh giá bất đẳng thức cơ bản để thu hẹp miền x, y rồi thay vào tìm trực tiếp.
Chọn đáp án A
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(2041200\).
B. \(2041204\).
C. \(2041195\).
D. \(2041207\).
Lời giải
Ta có \(g'\left( x \right) = \left( {4{x^3} - 4x} \right)f'\left( {{x^4} - 2{x^2} + m} \right)\) ; \(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}4{x^3} - 4x = 0{\rm{ }}\left( 1 \right)\\f'\left( {{x^4} - 2{x^2} + m} \right){\rm{ = 0 }}\left( 2 \right)\end{array} \right.\)
\(\left( 1 \right) \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\\x = 0\end{array} \right.\) .
\(\left( 2 \right) \Leftrightarrow \left[ \begin{array}{l}{x^4} - 2{x^2} + m = - 2\\{x^4} - 2{x^2} + m = - 1\\{x^4} - 2{x^2} + m = 3\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l} - m = {x^4} - 2{x^2} + 2 = {g_1}\left( x \right)\\ - m = {x^4} - 2{x^2} + 1 = {g_2}\left( x \right)\\ - m = {x^4} - 2{x^2} - 3 = {g_3}\left( x \right)\end{array} \right.\).
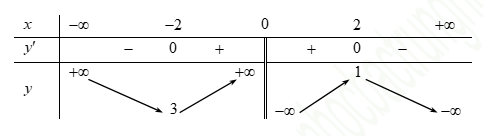
Ta có bảng biến thiên của các hàm số \({g_1}\left( x \right),{g_2}\left( x \right),{g_3}\left( x \right)\) như hình vẽ:

Từ bảng biến trên, ta dễ thấy: với \[ - m \le - 4 \Leftrightarrow m \ge 4\] hàm số \(g\left( x \right) = f\left( {{x^4} - 2{x^2} + m} \right)\) có đúng 3 điểm cực trị.
Do đó: \(S = \left\{ {4;5;6;7;...;2020} \right\}\)
Vậy tổng tất cả các phần tử của \(S\) là: \(4 + 5 + 6 + ... + 2020 = \frac{{\left( {4 + 2020} \right)2017}}{2} = 2041204\).
Chọn đáp án B
Câu 2
A. \(\frac{3}{{2\sqrt {15} }}\).
B. \(\frac{1}{{\sqrt {15} }}\).
C. \(\frac{{\sqrt {14} }}{{\sqrt {15} }}\).
D. \(\frac{{\sqrt {14} }}{{3\sqrt {15} }}\).
Lời giải
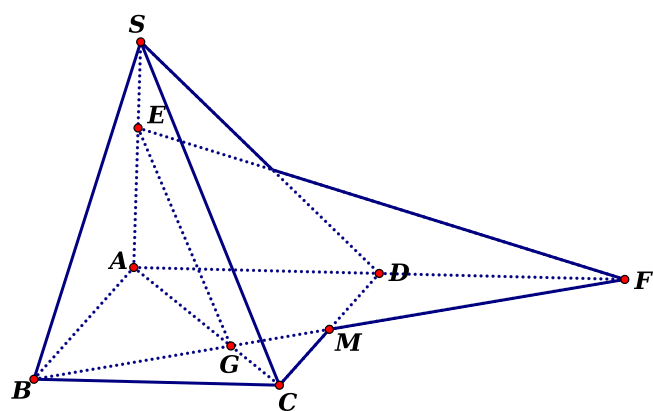
Góc giữa hai mặt phẳng
 và
và 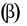 là góc
là góc 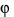 . Khi đó \(\sin \varphi = \frac{{d\left( {A,\alpha } \right)}}{{d\left( {A,\Delta } \right)}}\)
. Khi đó \(\sin \varphi = \frac{{d\left( {A,\alpha } \right)}}{{d\left( {A,\Delta } \right)}}\)
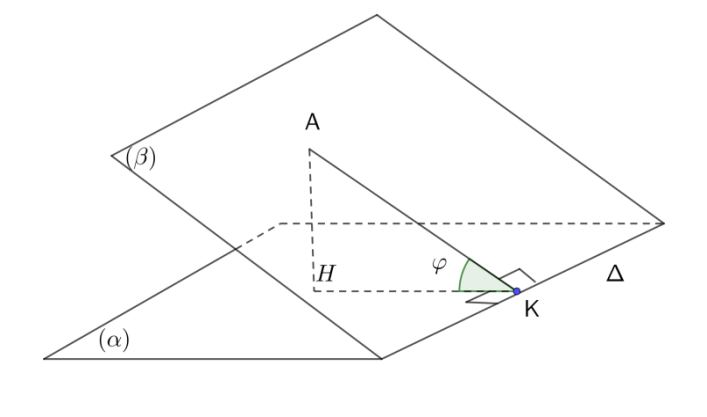
Gọi điểm 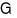 là trọng tâm
là trọng tâm 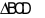 , kéo dài tia
, kéo dài tia 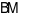 cắt
cắt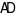 tại
tại 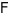 .
. 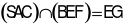 .
.
Khi đó góc giữa hai mặt phẳng\(\left( {SAC} \right)\) và \(\left( {BME} \right)\)là góc 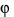 có\(\sin \varphi = \frac{{d\left( {A,\left( {{\rm{BEF}}} \right)} \right)}}{{d\left( {A,EG} \right)}}\) .
có\(\sin \varphi = \frac{{d\left( {A,\left( {{\rm{BEF}}} \right)} \right)}}{{d\left( {A,EG} \right)}}\) .
Ta có \(d\left( {A,\left( {{\rm{BEF}}} \right)} \right) = \frac{{2a\sqrt 3 }}{3}\),\(d\left( {A,EG} \right) = \frac{{AE.AG}}{{\sqrt {A{E^2} + A{G^2}} }} = \frac{{a\sqrt {70} }}{7}\)
\(\sin \varphi = \frac{{d\left( {A,\left( {{\rm{BEF}}} \right)} \right)}}{{d\left( {A,EG} \right)}} = \frac{{\sqrt {14} }}{{\sqrt {15} }} \to {\rm{cos}}\varphi {\rm{ = }}\frac{1}{{\sqrt {15} }}\).
Nhận xét:Bản chất câu 49 khó khăn nhất là việc xác định góc giữa hai mặt phẳng. Tứ diện \(S.ABC\)là một tứ diện đặc biệt được tách từ hình chóp \(S.ABCD\)có \(SD \bot \left( {ABCD} \right)\), mặt đáy là hình vuông. Đây là bài toán khá quen thuộc. Với những bài toán xác định góc phức tạp hơn các em học sinh có thể dùng phương pháp tọa độ.
Chọn đáp án B
Câu 3
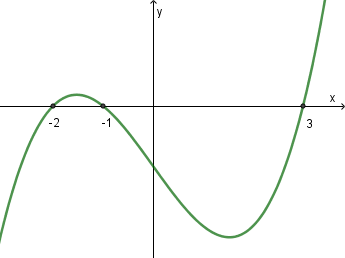
Cho hàm số \(y = \frac{{ax - 2}}{{cx + d}}\) có đồ thị như hình vẽ bên dưới
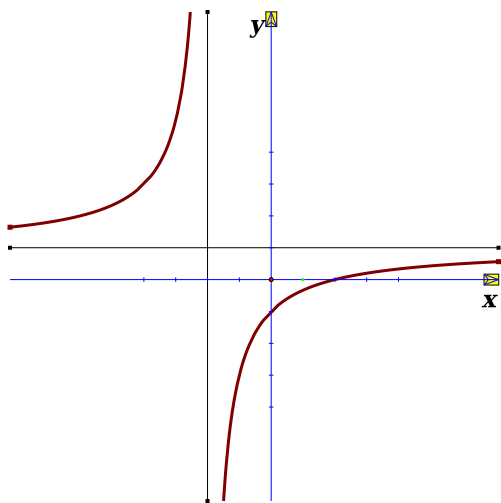
Mệnh đề nào sau đây đúng
A. \(a < 0,\,c < 0,\,d < 0\).
B. \(a < 0,\,c >0,\,d < 0\).
C. \(a >0,\,c >0,\,d >0\).
D. \(a >0,\,c < 0,\,d >0\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\frac{a}{b} \in \left( {2;3} \right)\).
B. \(\frac{a}{b} \in \left( {3;9} \right)\).
C. \(\frac{a}{b} \in \left( {0;2} \right)\).
D. \(\frac{a}{b} \in \left( {9;16} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A.\(\left( { - 2;\,2} \right)\).
B.\(\left( {0;\,2} \right)\).
C.\(\left( {3;\, + \infty } \right)\).
D.\(\left( { - \infty ;\,1} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(7879\) triệu người.
B. \(7680\) triệu người.
C. \(7782\) triệu người.
D. \(7777\) triệu người.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.