Câu hỏi:
02/05/2022 1,985Hình chóp \(S.ABCD\) có đáy là hình chữ nhật với \(AB = 3,BC = 4,SC = 5.\) Tam giác \(SAC\) nhọn và nằm trong mặt phẳng vuông góc với \(\left( {ABCD} \right).\) Các mặt \(\left( {SAB} \right)\) và \(\left( {SAC} \right)\) tạo với nhau một góc \(\alpha \) và \(\cos \alpha = \frac{3}{{\sqrt {29} }}.\) Tính thể tích khối chóp \(S.ABCD\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án C.
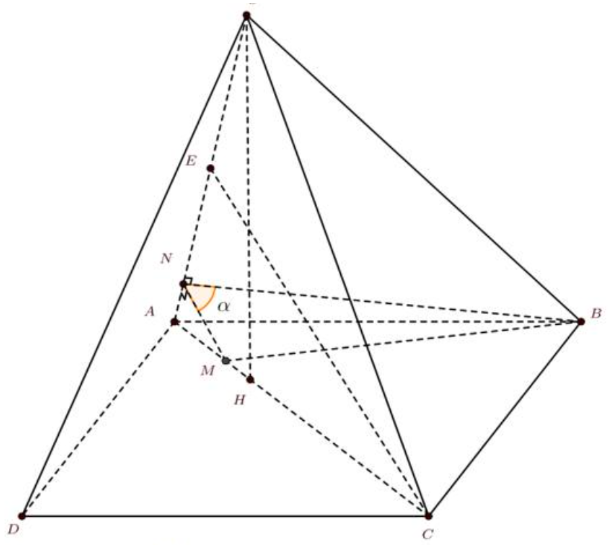
Kẻ \(SH \bot AC\left( {H \in AC} \right)\) vì \(\Delta SAC\) nhọn.
Ta có \(\left\{ \begin{array}{l}\left( {SAC} \right) \cap \left( {ABCD} \right) = AC\\SH \bot AC\end{array} \right. \Rightarrow SH \bot \left( {ABCD} \right).\)
Kẻ \(MB \bot AC \Rightarrow MB \bot \left( {SAC} \right) \Rightarrow MB \bot SA,\left( 1 \right).\)
Ta có \(AC = SC = 5\) nên \(\Delta SAC\) cân tại \(C.\)
Gọi \(E\) là trung điểm của \(SA\) nên \(SA \bot EC,\) kẻ \(MN//EC\left( {N \in SA} \right)\) nên \(SA \bot MN\left( 2 \right).\)
Từ (1), (2) suy ra \(SA \bot \left( {MNB} \right) \Rightarrow \widehat {BNM} = \alpha .\)
Ta có \(\frac{1}{{{{\cos }^2}\alpha }} = 1 + {\tan ^2}\alpha \Rightarrow \tan \alpha = \sqrt {\frac{1}{{{{\left( {\frac{3}{{\sqrt {29} }}} \right)}^2}}} - 1} = \frac{{2\sqrt 5 }}{3}.\)
Trong \(\Delta ABC:MB = \frac{{AB.BC}}{{\sqrt {A{B^2} + B{C^2}} }} = \frac{{12}}{5},AM = \sqrt {A{B^2} - M{B^2}} = \frac{9}{5}.\)
Trong \(\Delta BMN:MN = \frac{{MB}}{{\tan \alpha }} = \frac{{18\sqrt 5 }}{{25}}.\)
Trong \(\Delta SAC:\frac{{AM}}{{AC}} = \frac{{MN}}{{EC}} = \frac{{\frac{9}{5}}}{5} = \frac{9}{{25}}\) suy ra \(EC = \frac{{25MN}}{9} = 2\sqrt 5 .\)
Ta có \(SA = 2SE = 2\sqrt {S{C^2} - E{C^2}} = 2\sqrt 5 \)
Và \(SH.AC = SA.EC \Leftrightarrow SH = \frac{{SA.EC}}{{AC}} = \frac{{2\sqrt 5 .2\sqrt 5 }}{5} = 4.\)
Vậy thể tích khối chóp là \(V = \frac{1}{3}.SH.{S_{ABCD}} = \frac{1}{3}.4.3.4 = 16.\)
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án D.
Ta có \(1 - \cos 2x = 0 \Leftrightarrow \cos 2x = 1 \Leftrightarrow 2x = k2\pi \Leftrightarrow x = k\pi \left( {k \in \mathbb{Z}} \right).\)
Vậy tập nghiệm của phương trình là \(\left\{ {k\pi ,k \in \mathbb{Z}} \right\}.\)
Lời giải
Đáp án A.
Ta có \(y' = - \frac{1}{{{{\left( {x + 1} \right)}^2}}} < 0\) với mọi \(x \in \left[ {0;4} \right].\) Suy ra, hàm số luôn nghịch biến trên \(\left[ {0;4} \right].\)
Vậy \({y_{\min }} = y\left( 4 \right) = \frac{{11}}{5}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 19)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
45 bài tập Xác suất có lời giải