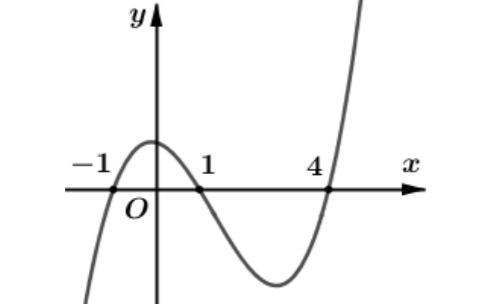
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a,SA \bot \left( {ABC} \right),\) góc giữa đường thẳng \(SB\) và mặt phẳng \(\left( {ABC} \right)\) bằng \({60^0}.\) Khoảng cách giữa hai đường thẳng \(AC\) và \(SB\) bằng:
A.\(\frac{{a\sqrt 3 }}{7}.\)
B.\(\frac{{a\sqrt 2 }}{2}.\)
C.\(\frac{{a\sqrt {15} }}{5}.\)
D. \(\frac{{a\sqrt 7 }}{7}.\)
Quảng cáo
Trả lời:
Đáp án C.
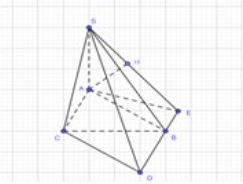
Trong mp \(\left( {ABC} \right)\) kẻ hình bình hành \(ABDC,AE \bot BD;\) trong mp \(\left( {SAE} \right)\) kẻ \(AH \bot SE.\)
Theo giả thiết:
\(\left\{ \begin{array}{l}SA \bot \left( {ABC} \right)\\AE \bot BD\end{array} \right. \Rightarrow SA \bot BD \Rightarrow BD \bot \left( {SAE} \right)\)
\( \Leftrightarrow BD \bot AH\) mà \(AH \bot SE\) nên \(AH \bot \left( {SBD} \right).\)
Ta lại có \(BD//AC \Rightarrow AC//\left( {SBD} \right) \Rightarrow d\left( {AC,SB} \right) = d\left( {AC,\left( {SBD} \right)} \right) = d\left( {A,\left( {ABD} \right)} \right) = AH\).
Mặt khác: Vì \(SA \bot \left( {ABC} \right)\) nên \(\widehat {\left( {SA,\left( {ABC} \right)} \right)} = \widehat {SBA} = {60^0},SA = AB.\tan {60^0} = a\sqrt 3 .\)
Vì \(ABDC\) là hình bình hành nên \(\widehat {ABD} = {180^0} - \widehat {BAC} = {120^0}\) do đó điểm \(E\) nằm ngoài đoạn thẳng \(BD\) và góc \(\widehat {ABE} = {60^0} \Rightarrow AE = AB\sin {60^0} = \frac{{a\sqrt 3 }}{2}.\)
Tam giác \(SAE\) vuông có:
\(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{E^2}}} = \frac{1}{{{{\left( {a\sqrt 3 } \right)}^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}} = \frac{5}{{3{a^2}}} \Rightarrow A{H^2} = \frac{{3{a^2}}}{5} \Rightarrow AH = \frac{{a\sqrt {15} }}{5}.\)
Vậy khoảng cách giữa 2 đường thẳng \(AC\) và \(SB\) là \(\frac{{a\sqrt {15} }}{5}.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án A.
Tập xác định: \(D = \mathbb{R}.\)
*) Nếu \(m = 0\) ta có \(y = 5x.\) Đồ thị hàm số luôn đồng biến trên \(\mathbb{R}.\)
*) Nếu \(m \ne 0.\) Ta có: \(y' = m{x^2} - 4mx + 3m + 5.\)
Hàm số đồng biến trên \(\mathbb{R} \Leftrightarrow y' \ge 0,\forall x \in \mathbb{R}.\)
\( \Leftrightarrow m{x^2} - 4mx + 3m + 5 \ge 0,\forall x \in \mathbb{R}.\)
\( \Leftrightarrow \left\{ \begin{array}{l}\Delta ' \le 0\\a >0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4{m^2} - m\left( {3m + 5} \right) \le 0\\m >0\end{array} \right..\)
\( \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 5m \le 0\\m >0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}0 \le m \le 5\\m >0\end{array} \right. \Leftrightarrow 0 < m \le 5\)
Kết hợp với điều kiện ta có: \(0 < m \le 5.\)
Vậy \(0 < m \le 5,m \in \mathbb{Z} \Rightarrow m \in \left\{ {0;1;2;3;4;5} \right\}.\)
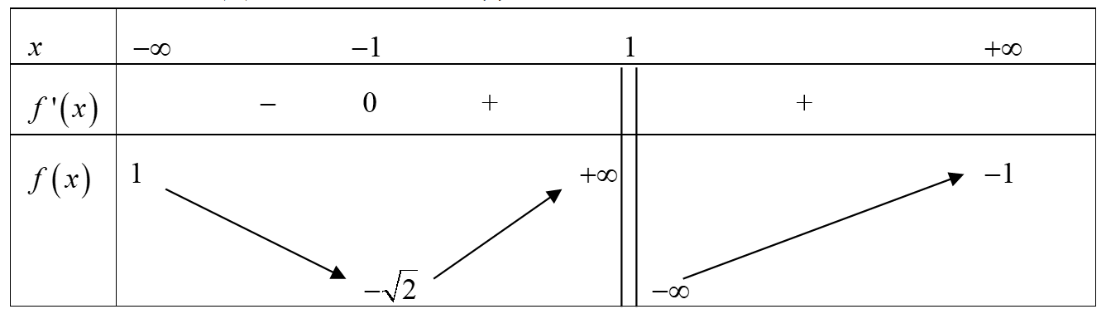
Câu 2
A.\(\left( {4;7} \right).\)
B.\(\left( { - 1;2} \right).\)
C.\(\left( {2;3} \right).\)
D.\(\left( { - \infty ; - 1} \right).\)
Lời giải
Đáp án B.
Ta có \(y = g\left( x \right) = f\left( {\left| {x - 3} \right|} \right) \Rightarrow y' = \frac{{x - 3}}{{\left| {x - 3} \right|}}.f'\left( {\left| {x - 3} \right|} \right).\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}\left| {x - 3} \right| = - 1\left( L \right)\\\left| {x - 3} \right| = 1\\\left| {x - 3} \right| = 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2 \vee x = 4\\x = - 1 \vee x = 7\end{array} \right.\) (Hàm số không có đạo hàm tại \(x = 3).\)
BBT
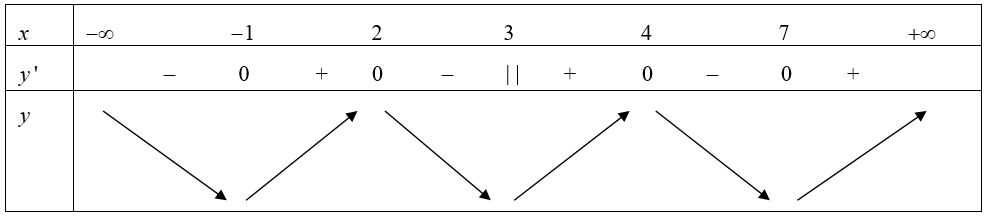
Vậy hàm số đồng biến trên khoảng \(\left( { - 1;2} \right).\)
Câu 3
A.\({30^0}.\)
B.\({60^0}.\)
C.\(\arcsin \frac{3}{5}.\)
D.\({45^0}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A.\(\frac{{\sqrt {21} }}{2}.\)
B.\(\frac{{\sqrt {21} }}{{14}}.\)
C.\(\frac{{\sqrt {21} }}{3}.\)
D. \(\frac{{\sqrt {21} }}{7}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
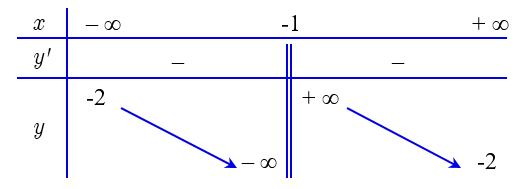
Câu 5
A.\(\left( { - 1;1} \right].\)
B.\(\left( { - \sqrt 2 ; - 1} \right).\)
C.\(\left( { - \sqrt 2 ; - 1} \right].\)
D. \(\left( { - 1;1} \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(y = \frac{{ - 2x + 3}}{{x + 1}}.\)
B. \(y = \frac{{ - 2x - 4}}{{x + 1}}.\)
C. \(y = \frac{{2 - x}}{{x + 1}}.\)
D. \(y = \frac{{x - 4}}{{2x + 2}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
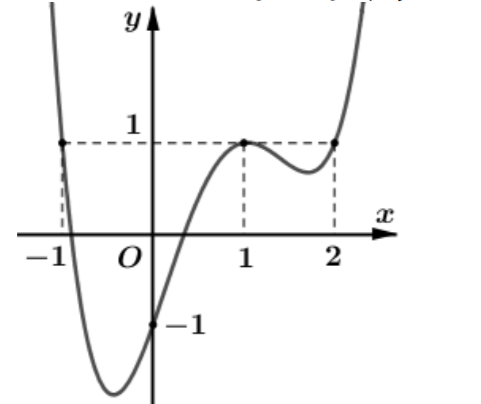
Câu 7
B.\(g\left( { - 1} \right) < g\left( 1 \right) < g\left( 2 \right).\)
C.\(g\left( 2 \right) < g\left( { - 1} \right) < g\left( 1 \right).\)
D.\(g\left( 1 \right) < g\left( { - 1} \right) < g\left( 2 \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.