2. Tốt nghiệp THPT
  3. Toán

Câu hỏi:

10/05/2022 339

Cho tứ diện đều ABCD có cạnh đáy bằng a, M là trung điểm của CD. Tính cosin của góc giữa hai đường thẳng AC, BM.  

Đáp án chính xác
Xem lời giải

Câu hỏi trong đề: Bộ đề thi thử môn Toán THPT Quốc gia năm 2022 có lời giải (30 đề) !!

Bắt đầu thi

Quảng cáo

Trả lời:

verified
Giải bởi Vietjack

Phương pháp:

- Gọi N là trung điểm của AD chứng minh ∠AC;BM=∠MN;BM

- Tính các cạnh của tam giác BMN sử dụng định lí Co-sin trong tam giác: cos∠BMN=BM2+MN2−BN22BM.MN

Cách giải:

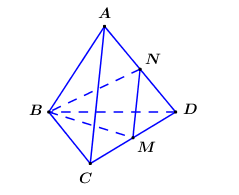
Cho tứ diện đều ABCD có cạnh đáy bằng a, M là trung điểm của CD (ảnh 1)

Gọi N là trung điểm của AD ta có MN//AC (MN là đường trung bình của ΔACD)

⇒∠AC;BM=∠MN;BM.

ΔABD,ΔBCD là các tam giác đều cạnh a nên BM=BN=a32.

MN là đường trung bình của ΔACD nên MN=12AC=a2.

Áp dụng định lí Co-sin trong tam giác BMN:cos∠BMN=BM2+MN2−BN22BM.MN=3a24+a24−3a242.a32.a2=36.

Chọn A.

Nhà sách vietjack
Xem thêm kho sách »

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

  1. 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
  2. 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
  3. Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
  4. Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )

Bình luận


Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Gọi S là tập hợp tất cả các số tự nhiên có 5 chữ số đôi một khác nhau. Chọn ngẫu nhiên một số thuộc S xác suất để số đó có hai chữ số tận cùng không có cùng tính chẵn lẻ bằng:

Xem đáp án » 12/05/2022 15,258

Câu 2:

Số nghiệm nguyên của bất phương trình ln2x+1≥1+lnx−1 là:

Xem đáp án » 09/05/2022 6,405

Câu 3:

Trong không gian Oxyz, mặt cầu có tâm I(4; -4; 2) và đi qua gốc tọa độ có phương trình là:

Xem đáp án » 09/05/2022 4,864

Câu 4:

Cho cấp số nhân un với u1=2 và u2=6. Công bội của cấp số nhân đã cho bằng:

Xem đáp án » 12/05/2022 4,836

Câu 5:

Cho đường thẳng y = 2x và parabol y=x2+c (c là tham số thực dương). Gọi S1 và S2 lần lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên. Khi S1=S2 thì c gần với số nào nhất sau đây?

Cho đường thẳng y = 2x và parabol y = x^2 + c (c là tham số thực dương) (ảnh 1)

Xem đáp án » 12/05/2022 3,272

Câu 6:

Có bao nhiêu giá trị nguyên của m thuộc đoạn [-10; 10] để hàm số y=2021−x+22021−x+m đồng biến trên khoảng 0;+∞?

Xem đáp án » 12/05/2022 3,055

Câu 7:

Trong không gian Oxyz, cho mặt cầu (S) có phương trình x2+y2+z2−4x+2y−6z−2=0. Tọa độ tâm I và bán kính R của mặt cầu là:

Xem đáp án » 12/05/2022 2,856
Xem thêm các câu hỏi khác »
Hỏi bài tập
Vietjack official store
Đăng ký gói thi VIP

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

  • Được thi tất cả các đề của các lớp có trên Khoahoc.vietjack.com
  • Ngân hàng câu hỏi trắc nghiệm theo các mức độ Nhận biết, Thông hiểu, Vận dụng, Vận dụng cao.
  • Luyện chuyên sâu, rèn tốc độ với trọn bộ đề thi thử, đề minh họa, chính thức các năm.
  • Hỏi bài tập với đội ngũ chuyên môn cao của chúng tôi.

Đặt mua

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

  • Được thi tất cả các đề của các lớp có trên Khoahoc.vietjack.com
  • Ngân hàng câu hỏi trắc nghiệm theo các mức độ Nhận biết, Thông hiểu, Vận dụng, Vận dụng cao.
  • Luyện chuyên sâu, rèn tốc độ với trọn bộ đề thi thử, đề minh họa, chính thức các năm.
  • Hỏi bài tập với đội ngũ chuyên môn cao của chúng tôi.

Đặt mua

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

  • Được thi tất cả các đề của các lớp có trên Khoahoc.vietjack.com
  • Ngân hàng câu hỏi trắc nghiệm theo các mức độ Nhận biết, Thông hiểu, Vận dụng, Vận dụng cao.
  • Luyện chuyên sâu, rèn tốc độ với trọn bộ đề thi thử, đề minh họa, chính thức các năm.
  • Hỏi bài tập với đội ngũ chuyên môn cao của chúng tôi.

Đặt mua

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

  • Siêu tiết kiệm - Được thi tất cả các đề của các lớp có trên Khoahoc.vietjack.com
  • Ngân hàng câu hỏi trắc nghiệm theo các mức độ Nhận biết, Thông hiểu, Vận dụng, Vận dụng cao.
  • Luyện chuyên sâu, rèn tốc độ với trọn bộ đề thi thử, đề minh họa, chính thức các năm.
  • Hỏi bài tập với đội ngũ chuyên môn cao của chúng tôi.

Đặt mua

🔥 Đề thi HOT:

  1. 2696 người thi tuần này

    (2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
  2. 2591 người thi tuần này

    30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
  3. 1251 người thi tuần này

    Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
  4. 542 người thi tuần này

    (2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
  5. 481 người thi tuần này

    45 bài tập Xác suất có lời giải
  6. 433 người thi tuần này

    Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
  7. 371 người thi tuần này

    50 bài tập Nguyên hàm, tích phân và ứng dụng có lời giải
  8. 286 người thi tuần này

    CÂU TRẮC NGHIỆM ĐÚNG SAI

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack25. All Rights Reserved.

Đăng ký

Bạn đã có tài khoản?