Câu hỏi:

12/05/2022 204

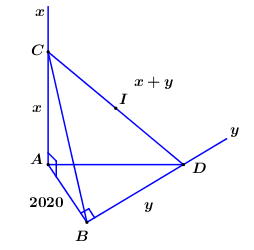
Cho hai đường thẳng x'x, y'y chéo nhau và vuông góc với nhau. Trên x'x lấy cố định điểm A, trên y'y lấy cố định điểm B sao cho AB cùng vuông góc với Ax, By và AB = 2020 cm. Gọi CD là hai điểm lần lượt di chuyển trên hai tia Ax, By sao cho AC + BD = AD. Hỏi bán kính R của mặt cầu (S) ngoại tiếp tứ diện ABCD có giá trị nhỏ nhất thuộc khoảng nào sau đây?

A. (1009; 1011)

B. (1427; 1429)

Đáp án chính xác

C. (2855; 2857)

D. (2019; 2021)

Xem lời giải

Câu hỏi trong đề: Bộ đề thi thử môn Toán THPT Quốc gia năm 2022 có lời giải (30 đề) !!

Trả lời:

Giải bởi Vietjack

Phương pháp:

- Đặt $A C = x, B D = y (x, y > 0) \Rightarrow C D = x + y .$

- Sử dụng định lí Pytago tìm xy.

- Gọi I là trung điểm của CD. Chứng minh I là tâm mặt cầu ngoại tiếp tứ diện ABCD.

- Áp dụng BĐT Cô-si.

Cách giải:

Cho hai đường thẳng x'x, y'y chéo nhau và vuông góc với nhau. Trên x'x (ảnh 1)

Ta có: $\{\begin{cases} A C ⊥ B D \\ A C ⊥ A B \end{cases} \Rightarrow A C ⊥ (A B D) .$

Đặt $A C = x, B D = y (x, y > 0) \Rightarrow C D = x + y .$

Áp dụng định lí Pytago ta có:

$A D^{2} = 2020^{2} + y^{2}$

$C D^{2} = A C^{2} + A D^{2}$

$\Rightarrow {(x + y)}^{2} = x^{2} + 2020^{2} + y^{2}$

$\Rightarrow x y = \frac{2020^{2}}{2}$

Gọi I là trung điểm của CD.

Ta có: $\{\begin{cases} B D ⊥ A B \\ B D ⊥ A C \end{cases} \Rightarrow B D ⊥ (A B C) \Rightarrow B D ⊥ B C .$

Vì $Δ A C D, Δ B C D$ là các tam giác vuông tại A, B nên $I A = I B = \frac{1}{2} C D = I C = I D \Rightarrow I$ là tâm mặt cầu ngoại tiếp khối chóp ABCD bán kính $R = \frac{1}{2} C D .$

Ta có $R = \frac{1}{2} C D = \frac{x + y}{2} \geq \sqrt{x y} = \sqrt{\frac{2020^{2}}{2}} \approx 1428, 355.$

Chọn B.

Bình luận hoặc Báo cáo
về câu hỏi!

Câu 1:

Gọi S là tập hợp tất cả các số tự nhiên có 5 chữ số đôi một khác nhau. Chọn ngẫu nhiên một số thuộc S xác suất để số đó có hai chữ số tận cùng không có cùng tính chẵn lẻ bằng:

A. $\frac{4}{9}$

B. $\frac{5}{9}$

C. $\frac{3}{5}$

D. $\frac{2}{5}$

Xem đáp án » 12/05/2022 11,983

Câu 2:

Số nghiệm nguyên của bất phương trình $\ln (2 x + 1) \geq 1 + \ln (x - 1)$ là:

A. 5

B. Vô số

C. 6

D. 4

Xem đáp án » 09/05/2022 5,372

Câu 3:

Trong không gian Oxyz, mặt cầu có tâm I(4; -4; 2) và đi qua gốc tọa độ có phương trình là:

A. ${(x + 4)}^{2} + {(y - 4)}^{2} + {(z + 2)}^{2} = 6$

B. ${(x + 4)}^{2} + {(y - 4)}^{2} + {(z + 2)}^{2} = 36$

C. ${(x - 4)}^{2} + {(y + 4)}^{2} + {(z - 2)}^{2} = 36$

D. ${(x - 4)}^{2} + {(y + 4)}^{2} + {(z - 2)}^{2} = 6$

Xem đáp án » 09/05/2022 3,736

Câu 4:

Có bao nhiêu giá trị nguyên của m thuộc đoạn [-10; 10] để hàm số $y = \frac{2021^{- x} + 2}{2021^{- x} + m}$ đồng biến trên khoảng $(0; + \infty) ?$

A. 11

B. 3

C. 13

D. 2

Xem đáp án » 12/05/2022 2,831

Câu 5:

Cho cấp số nhân $(u_{n})$ với $u_{1} = 2$ và $u_{2} = 6.$ Công bội của cấp số nhân đã cho bằng:

A. 4

B. 3

C. 8

D. 12

Xem đáp án » 12/05/2022 2,348

Câu 6:

Trong không gian Oxyz, cho mặt cầu (S) có phương trình $x^{2} + y^{2} + z^{2} - 4 x + 2 y - 6 z - 2 = 0.$ Tọa độ tâm I và bán kính R của mặt cầu là:

A. $I (2; - 1; 3), R = \sqrt{14} .$

B. $I (- 2; 1; - 3), R = \sqrt{14} .$

C. $I (2; - 1; 3), R = 4.$

D. $I (- 2; 1; - 3), R = 4.$

Xem đáp án » 12/05/2022 2,301

Câu 7:

Giá trị nhỏ nhất của hàm số $f (x) = - x^{4} + 12 x^{2} + 1$ trên đoạn [1; 2] bằng:

A. 1

B. 33

C. 12

D. 0

Xem đáp án » 12/05/2022 2,213

Xem thêm các câu hỏi khác »

Nhà sách VIETJACK:

Gọi S là tập hợp tất cả các số tự nhiên có 5 chữ số đôi một khác nhau. Chọn ngẫu nhiên một số thuộc S xác suất để số đó có hai chữ số tận cùng không có cùng tính chẵn lẻ bằng:

Số nghiệm nguyên của bất phương trình $\ln (2 x + 1) \geq 1 + \ln (x - 1)$ là:

Trong không gian Oxyz, mặt cầu có tâm I(4; -4; 2) và đi qua gốc tọa độ có phương trình là:

Có bao nhiêu giá trị nguyên của m thuộc đoạn [-10; 10] để hàm số $y = \frac{2021^{- x} + 2}{2021^{- x} + m}$ đồng biến trên khoảng $(0; + \infty) ?$

Cho cấp số nhân $(u_{n})$ với $u_{1} = 2$ và $u_{2} = 6.$ Công bội của cấp số nhân đã cho bằng:

Trong không gian Oxyz, cho mặt cầu (S) có phương trình $x^{2} + y^{2} + z^{2} - 4 x + 2 y - 6 z - 2 = 0.$ Tọa độ tâm I và bán kính R của mặt cầu là:

Giá trị nhỏ nhất của hàm số $f (x) = - x^{4} + 12 x^{2} + 1$ trên đoạn [1; 2] bằng:

Bình luận

🔥 Đề thi HOT:

VIP +3 tháng ( 199,000 VNĐ )

VIP +6 tháng ( 299,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

Nhà sách VIETJACK:

Gọi S là tập hợp tất cả các số tự nhiên có 5 chữ số đôi một khác nhau. Chọn ngẫu nhiên một số thuộc S xác suất để số đó có hai chữ số tận cùng không có cùng tính chẵn lẻ bằng:

Số nghiệm nguyên của bất phương trình ln2x+1≥1+lnx−1 là:

Trong không gian Oxyz, mặt cầu có tâm I(4; -4; 2) và đi qua gốc tọa độ có phương trình là:

Có bao nhiêu giá trị nguyên của m thuộc đoạn [-10; 10] để hàm số y=2021−x+22021−x+m đồng biến trên khoảng 0;+∞?

Cho cấp số nhân un với u1=2 và u2=6. Công bội của cấp số nhân đã cho bằng:

Trong không gian Oxyz, cho mặt cầu (S) có phương trình x2+y2+z2−4x+2y−6z−2=0. Tọa độ tâm I và bán kính R của mặt cầu là:

Giá trị nhỏ nhất của hàm số fx=−x4+12x2+1 trên đoạn [1; 2] bằng:

Bình luận

🔥 Đề thi HOT:

VIP +3 tháng ( 199,000 VNĐ )

VIP +6 tháng ( 299,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Số nghiệm nguyên của bất phương trình $\ln (2 x + 1) \geq 1 + \ln (x - 1)$ là:

Có bao nhiêu giá trị nguyên của m thuộc đoạn [-10; 10] để hàm số $y = \frac{2021^{- x} + 2}{2021^{- x} + m}$ đồng biến trên khoảng $(0; + \infty) ?$

Cho cấp số nhân $(u_{n})$ với $u_{1} = 2$ và $u_{2} = 6.$ Công bội của cấp số nhân đã cho bằng:

Trong không gian Oxyz, cho mặt cầu (S) có phương trình $x^{2} + y^{2} + z^{2} - 4 x + 2 y - 6 z - 2 = 0.$ Tọa độ tâm I và bán kính R của mặt cầu là:

Giá trị nhỏ nhất của hàm số $f (x) = - x^{4} + 12 x^{2} + 1$ trên đoạn [1; 2] bằng: