Câu hỏi:
20/05/2022 2,299
Đọc đoạn trích sau đây và trả lời các câu hỏi:
Con Sông Đà tuôn dài tuôn dài như một áng tóc trữ tình, đầu tóc chân tóc ẩn hiện trong mây trời tây Bắc bung nở hoa ban hoa gạo tháng hai va cuồn cuộn mù khói Mèo đốt nương xuân. Tôi đã nhìn say sưa làn mây mùa xuân bay trên Sông Đà, tôi đã xuyên qua đám mây mùa thu mà nhìn xuống dòng nước Sông Đà. Mùa xuân dòng xanh ngọc bích, chứ nước Sông Đà không xanh màu xanh canh hến của Sông Gâm Sông Lô. Mùa thu nước Sông đà lừ lừ chín đỏ như da mặt một người bầm đi vì rượu bữa, lừ lừ cái màu đỏ giận dữ ở một người bất mãn bực bội gì mỗi độ thu về.
(Trích Người lái đò Sông Đà – Nguyễn Tuân, Ngữ văn 12, Tập một, NXB Giáo dục)
Nội dung của đoạn trích trên là gì?
Đọc đoạn trích sau đây và trả lời các câu hỏi:
Con Sông Đà tuôn dài tuôn dài như một áng tóc trữ tình, đầu tóc chân tóc ẩn hiện trong mây trời tây Bắc bung nở hoa ban hoa gạo tháng hai va cuồn cuộn mù khói Mèo đốt nương xuân. Tôi đã nhìn say sưa làn mây mùa xuân bay trên Sông Đà, tôi đã xuyên qua đám mây mùa thu mà nhìn xuống dòng nước Sông Đà. Mùa xuân dòng xanh ngọc bích, chứ nước Sông Đà không xanh màu xanh canh hến của Sông Gâm Sông Lô. Mùa thu nước Sông đà lừ lừ chín đỏ như da mặt một người bầm đi vì rượu bữa, lừ lừ cái màu đỏ giận dữ ở một người bất mãn bực bội gì mỗi độ thu về.
(Trích Người lái đò Sông Đà – Nguyễn Tuân, Ngữ văn 12, Tập một, NXB Giáo dục)
Nội dung của đoạn trích trên là gì?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Phương pháp giải:
Căn cứ vào nội dung của tác phẩm
Giải chi tiết:
Đoạn trích trên nói đến vẻ đẹp trữ tình thơ mộng của con Sông Đà.
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: \(\frac{{a\sqrt 6 }}{6}\)
Phương pháp giải:
- Gọi M là trung điểm của BC, trong (SOM) kẻ \(OH \bot SM{\mkern 1mu} {\mkern 1mu} \left( {H \in SM} \right)\), chứng minh \(OH \bot \left( {SBC} \right)\).
- Áp dụng định lí Pytago và hệ thức lượng trong tam giác vuông tính khoảng cách.
Giải chi tiết:
Gọi M là trung điểm của BC, suy ra OM là đường trung bình của tam giác ABC.
\( \Rightarrow OM\parallel AB\), mà \(AB \bot BC\)\( \Rightarrow OM \bot BC\) và \(OM = \frac{1}{2}AB = \frac{a}{2}\).
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{BC \bot OM}\\{BC \bot SO{\mkern 1mu} {\mkern 1mu} \left( {SO \bot \left( {ABCD} \right)} \right)}\end{array}} \right.\)\( \Rightarrow BC \bot \left( {SOM} \right)\)
Trong (SOM) kẻ \(OH \bot SM{\mkern 1mu} {\mkern 1mu} \left( {O \in SM} \right)\), ta có:
\(\left\{ {\begin{array}{*{20}{l}}{BC \bot \left( {SOM} \right) \Rightarrow BC \bot OH}\\{OH \bot SM}\end{array}} \right.\)\( \Rightarrow OH \bot \left( {SBC} \right)\)
\( \Rightarrow d\left( {O;\left( {SBC} \right)} \right) = OH\).
Tam giác SBC đều cạnh a nên \(SM = \frac{{a\sqrt 3 }}{2}\).
Áp dụng định lí Pytago trong tam giác vuông SOM có: .
Áp dụng hệ thức lượng trong tam giác vuông SOM có: \(OH = \frac{{SO.OM}}{{SM}} = \frac{{\frac{a}{{\sqrt 2 }}.\frac{a}{2}}}{{\frac{{a\sqrt 3 }}{2}}} = \frac{{a\sqrt 6 }}{6}\).
Vậy \(d\left( {O;\left( {SBC} \right)} \right) = \frac{{a\sqrt 6 }}{6}\).
Lời giải
Phương pháp giải:
CSC \(\left( {{u_n}} \right)\)có tổng \(n\) số hạng đầu: \({S_n} = {u_1} + {u_2} + ... + {u_n} = \frac{{n\left( {{u_1} + {u_n}} \right)}}{2}\)
Giải chi tiết:
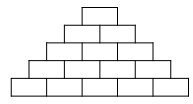
Tổng số viên gạch: \(S = 1 + 2 + ... + 500 = \frac{{500.\left( {1 + 500} \right)}}{2} = 125250\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 30)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 3)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận